
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,若AB=6,tan∠CDA= ![]() ,依题意补全图形并求DE的长.
,依题意补全图形并求DE的长.
【答案】
(1)证明:连OD,OE,如图1所示,
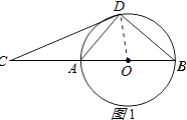
∵AB为直径,
∴∠ADB=90°,
即∠ADO+∠BDO=90°,
又∵∠CDA=∠CBD,
而∠CBD=∠BDO,
∴∠BDO=∠CDA,
∴∠CDA+∠ADO=90°,
即∠CDO=90°,
∴CD⊥OD,
∴CD是⊙O的切线
(2)解:如图2所示:

∵EB为⊙O的切线,
∴ED=EB,OE⊥DB,
∴∠ABD+∠DBE=90°,∠OEB+∠DBE=90°,
∴∠ABD=∠OEB,
∴∠CDA=∠OEB.
而tan∠CDA= ![]() ,
,
∴tan∠OEB= ![]() =
= ![]() ,
,
∵Rt△CDO∽Rt△CBE,
∴ ![]() =
= ![]() ,
,
∴CD= ![]() ×6=4,
×6=4,
在Rt△CBE中,设BE=x,
∴(x+4)2=x2+62,
解得:x= ![]() .
.
即BE的长为 ![]() ,
,
∴DE=BE= ![]() .
.
【解析】(1)连OD,OE.由AB为直径可得出∠ADO+∠BDO=90°,再根据圆周角定理和已知可得到∠CDA+∠ADO=90°,进而可证出结论;
(2)由切线的性质和已知可得到∠CDA=∠OEB,进而可得![]() ,再由Rt△CDO∽Rt△CBE可求出CD的长,在Rt△CBE中利用勾股定理可求出BE的长,即可得到DE的长.
,再由Rt△CDO∽Rt△CBE可求出CD的长,在Rt△CBE中利用勾股定理可求出BE的长,即可得到DE的长.
【考点精析】本题主要考查了相似三角形的性质和锐角三角函数的定义的相关知识点,需要掌握对应角相等,对应边成比例的两个三角形叫做相似三角形;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线 ![]() 经过点A(0,2)和B(1,
经过点A(0,2)和B(1, ![]() ).
).
(1)求该抛物线的表达式;
(2)已知点C与点A关于此抛物线的对称轴对称,点D在抛物线上,且点D的横坐标为4,求点C与点D的坐标;
(3)在(2)的条件下,将抛物线在点A,D之间的部分(含点A,D)记为图象G,如果图象G向下平移t(t>0)个单位后与直线BC只有一个公共点,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() , 下列说法正确的是( )
, 下列说法正确的是( )
A.图象经过点(2,﹣1)
B.图象位于第二、四象限
C.当x<0时,y随x的增大而减小
D.当x>0时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=x+2与双曲线 ![]() 相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.
相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.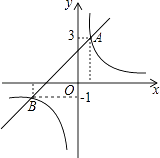
(1)求k的值;
(2)若y1<y2 , 请你根据图象确定x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节约用水,某市规定三口之家每月标准用水量为15立方米,单价为1.5元/立方米,超过部分单价为3元/立方米,某三口之家当月用水![]() 立方米(
立方米(![]() 且为整数)
且为整数)
⑴.请用正式表示用水![]() 立方米的费用;
立方米的费用;
⑵.三口之家当月缴水费37.50元,这月用了多少立方米的水.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题:
(1)(﹣1)2018﹣2(π﹣1)0+(﹣![]() )﹣2
)﹣2
(2)(2a﹣4)(![]() a+5)﹣2(a﹣10)
a+5)﹣2(a﹣10)
(3)(2x+3y)(﹣2x+3y)﹣(x﹣3y)2
(4)(4x3y﹣6x2y2+12xy3)÷2xy
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线G1:y=ax2+bx+c的顶点为(2,﹣3),且经过点(4,1).
(1)求抛物线G1的解析式;
(2)将抛物线G1先向左平移3个单位,再向下平移1个单位后得到抛物线G2 , 且抛物线G2与x轴的负半轴相交于A点,求A点的坐标;
(3)如果直线m的解析式为 ![]() ,点B是(2)中抛物线G2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n过点A和点B.问:是否存在点B,使直线m、n、x轴围成的三角形和直线m、n、y轴围成的三角形相似?若存在,求出点B的坐标;若不存在,请说明理由.
,点B是(2)中抛物线G2上的一个点,且在对称轴右侧部分(含顶点)上运动,直线n过点A和点B.问:是否存在点B,使直线m、n、x轴围成的三角形和直线m、n、y轴围成的三角形相似?若存在,求出点B的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=kx经过点A,点A在第四象限,过点A作AH⊥x轴,垂足为点H,点A的横坐标为3,且△AOH的面积为3.
(1)求正比例函数的解析式;
(2)在x轴上能否找到一点P,使△AOP的面积为5?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com