练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】根据表中的信息判断，下列语句中正确的是

    （　　）

    A.＝1.59

    B.235的算术平方根比15.3小

    C.只有3个正整数n满足

    D.根据表中数据的变化趋势，可以推断出16.12将比256增大3.19

    【答案】C

    【解析】

    据表格中的信息可知x2和其对应的算术平方根的值，然后依次判断各选项即可．

    A．根据表格中的信息知：，

    ∴＝1.59，故选项不正确；

    B．根据表格中的信息知：，

    ∴235的算术平方根比15.3大，故选项不正确；

    C．根据表格中的信息知：15.52＝240.25＜n＜15.62＝243.36，

    ∴正整数n＝241或242或243，

    ∴只有3个正整数n满足，故选项正确；

    D．根据表格中的信息无法得知16.12的值，

    ∴不能推断出16.12将比256增大3.19，故选项不正确．

    故选C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣ x2+bx+e与x轴交于点A（﹣3，0）、点B（9，0），与y轴交于点C，顶点为D，连接AD、DB，点P为线段AD上一动点．
    （1）求抛物线的解析式；
    （2）如图1，过点P作BD的平行线，交AB于点Q，连接DQ，设AQ=m，△PDQ的面积为S，求S关于m的函数解析式，以及S的最大值；

    （3）如图2，抛物线对称轴与x轴交与点G，E为OG的中点，F为点C关于DG对称的对称点，过点P分别作直线EF、DG的垂线，垂足为M、N，连接MN，直接写出△PMN为等腰三角形时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察图中给出的信息，回答下列问题：

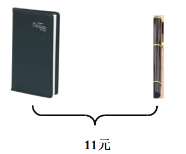
    （1）一本笔记本与一支中性笔分别是多少元？

    （2）某学校给参加体育比赛获一等奖的10名学生发笔记本，给获二等奖的20名学生发中性笔，现有两个超市在搞促销活动，A超市规定：这两种商品都打八折；B超市规定：每买一个笔记本送一支中性笔，另外购买的中性笔按原价卖．该学校选择哪家超市购买更合算，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】完成下面的证明：

    如图，BE平分∠ABD，DE平分∠BDC，且∠α+∠β=90°，求证：AB∥CD．

    证明：∵BE平分∠ABD(已知)，∴∠ABD=2∠α(　　)

    ∵DE平分∠BDC(　　)

    ∴∠BDC=　　(　　)，∴∠ABD+∠BDC=2∠α+2∠β=2(∠α+∠β)(等量代换)

    ∵∠α+∠β=90°(已知)，∴∠ABD+∠BDC=(　　)，∴AB∥CD(　　)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．

    小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．

    (1)按小明的思路，易求得∠APC的度数为_____度；

    (2)问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；

    (3)在(2)的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，顶点C的坐标为（﹣3，3 ），反比例函数y= 的图象与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解：材料一：对于任意的非零实数和正实数，如果满足是整数，则称是的一个“整商系数”， 例如：时 ，则是的一个“整商系数”；时， ，则也是的一个“整商系数”；

    结论：一个非零实数有无数个整商系数，其中最小的一个整商系数记为，例如： ．

    材料二：对于一元二次方程中，两根有如下关系：， 应用：

    （1）若实数满足，求的取值范围；

    （2）关于的方程的两个根分别为，且满足， 则的值为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】足球是世界第一运动，参与足球运动可以锻炼身体，陶冶情操．“高新美少年，阳春蹴鞠忙”，让学生走出教室，走进阳光，让每一位学生健康、快乐成长，是高新一中初中校区一直秉承的理念．本月，我校第四届校园足球联赛落下了帷幕，并取得了四满成功．为了举办本次活动，我校在商场购买甲、乙两种不同的足球，购买甲种足球共花费2600元，购买乙种足球共花费1328元，购买甲种足球的数量是购买乙种足球数量的2.5倍，且购买一个乙种足球比购买一个甲种足球多花18元．求购买一个甲种足球、一个乙种足球各需多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】骑自行车旅行越来越受到人们的喜爱，各种品牌的山地自行车相继投放市场，顺风车经营的A型车去年6月份销售总额为3.2万元，今年经过改造升级后A型车每辆销售价比去年增加400元，若今年6月份与去年6月份卖出的A型车数量相同，则今年6月份A型车销售总额将比去年6月份销售总额增加25%．
    A，B两种型号车的进货和销售价格表：

    A型车

    B型车

    进货价格（元/辆）

    1100

    1400

    销售价格（元/辆）

    今年的销售价格

    2400


    （1）求今年6月份A型车每辆销售价多少元；
    （2）该车行计划7月份新进一批A型车和B型车共50辆，且B型车的进货数量不超过A型车数量的两倍，应如何进货才能使这批车获利最多？

    查看答案和解析>>

    同步练习册答案