
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s). 
(1)当t=时,点E落在△MBC的边上;
(2)以E为圆心,1cm为半径作圆E,则当t=时,圆E与直线AB或直线CM相切.
【答案】
(1)![]()
(2)![]() ;
; ![]() ;5
;5
【解析】解:(1)如图1,∵四边形PCDE是正方形, 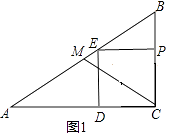
∴DP∥AC,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
解得t= ![]() ;(2)如图2,当点E在△ABC的内部时,圆E与直线AB相切,EF⊥
;(2)如图2,当点E在△ABC的内部时,圆E与直线AB相切,EF⊥
AB,且EF=1时,
连接AE、BE、CE,
∵∠ACB=90°,AC=8,BC=6,
∴AB=10,![]() ×AB×EF+
×AB×EF+ ![]() +
+ ![]() ×BC×EP=
×BC×EP= ![]() ×AC×BC,
×AC×BC,![]() ×10×1+
×10×1+ ![]() ×8×t+
×8×t+ ![]() ×6×t=
×6×t= ![]() ×8×6,
×8×6,
解得t= ![]() ;
;
如图3,当点E在△ABC的外部时,圆E与直线AB相切,EG⊥AB,且EG=1时,
∵∠EGH=∠BPH,∠EHG=∠BHP,
∴∠GEH=∠PBH,
∴cos∠GEH=cos∠ABC= ![]() =
= ![]() ,又EG=1,
,又EG=1,
∴EH= ![]() ,
,
∵ ![]() =
= ![]() ,∴HP=
,∴HP= ![]() ,
,
则 ![]() +
+ ![]() =t,
=t,
解得t= ![]() ;
;
如图4,当圆E与直线CM相切时,EN=1,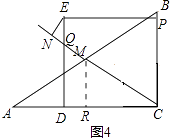
作MR∥BC,则MR= ![]() BC=3,CR=
BC=3,CR= ![]() AC=4,
AC=4,
∵点M是边AB的中点,
∴CM= ![]() AB=5,
AB=5,
tan∠ACM= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,CD=t,
,CD=t,
则QD= ![]() t,EQ=
t,EQ= ![]() t,
t,
∵∠NEQ=∠ACM,
∴ ![]() =
= ![]() =
= ![]() ,
,
解得t=5.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】将形状、大小完全相同的两个等腰三角形如图所示放置,点D在AB边上,△DEF绕点D旋转,腰DF和底边DE分别交△CAB的两腰CA,CB于M,N两点,若CA=5,AB=6,AD:AB=1:3,则MD+ ![]() 的最小值为 .
的最小值为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
则下列判断正确的是( )
A.抛物线开口向上
B.抛物线与y轴交于负半轴
C.当x=4时,y>0
D.方程ax2+bx+c=0的正根在3与4之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y= ![]() 的图象交斜边OB于点Q,
的图象交斜边OB于点Q,
(1)当Q为OB中点时,AP:PB=
(2)若P为AB的三等分点,当△AOQ的面积为 ![]() 时,k的值为
时,k的值为 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=1,BC= ![]() ,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC= .
,点O为Rt△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,则OA+OB+OC= . 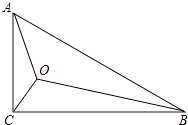
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校有学生2000名,为了了解学生在篮球、足球、排球和乒乓球这四项球类运动中最喜爱的一项球类运动情况,对学生开展了随机调查,丙将结果绘制成如下的统计图.
请根据以上信息,完成下列问题:
(1)本次调查的样本容量是 ;
(2)某位同学被抽中的概率是 ;
(3)据此估计全校最喜爱篮球运动的学生人数约有 名;
(4)将条形统计图补充完整.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com