
����Ŀ������ijУΪ����ѧ���Ŀ�������ḻ��ʣ���չ�����¿�����
���� | ����� |
A | �������� |
B | ��ѧ��Ȥ������ |
C | Ӣ���Ķ���д�� |
D | ������ |
E | ���� |
Ϊ�˽�ѧ����ѡ��������ִӸ�У�����ȡ�˲���ѧ�������ʾ����飨�����ʾ������ÿ��ѧ��ֻ��ѡ������һ��������ݵ���õ������ݻ�������ͼ��ʾ��������������ͳ��ͼ�������ͳ��ͼ�ṩ����Ϣ�ش��������⣨Ҫ��д����Ҫ�Ľ����̣���
��1���˴ι������� ��ѧ����
��2��������ͳ��ͼ����������
��3������ѧ��Ȥ���������������ε�Բ�ĽǵĶ���Ϊ ��
��4������У����2000��ѧ��������Ƹ�Уϲ��A��B��C������ѧ�����ж����ˣ�
��5��ѧУ����ϲ����A������ѧ����ѡȡ4λͬѧ������Ů��2��������2�����μ�У����Ͳ�����г�����������ȷ������ͬѧ�μӾ����������б�����״ͼ�ķ���������պ�һ��һŮ�μӾ����ĸ��ʣ�
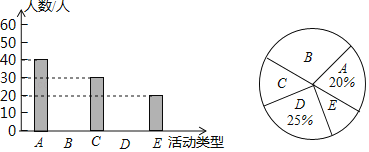
���𰸡���1��200����2������������3��108������4��1300����5��![]()
��������
��1����A����������A����ռ�ٷֱȼ��ɵõ��𰸣�
��2�����ɣ�1�����D�������������B���������Ӷ���ȫͼ�Σ�
��3����360����������ѧ��Ȥ����������ռ�ٷֱȼ��ɵõ��𰸣�
��4��2000���Ե�����ϲ��A��B��C������ѧ���İٷֱȣ����ɵõ��𰸣�
��5���Ȼ���״ͼ�������ø��ʹ�ʽ�����ɵõ���.
�⣺��1���˴ε����������Ϊ![]() ���ˣ���
���ˣ���
�ʴ�Ϊ��200��
��2��D��������Ϊ![]() ���ˣ���
���ˣ���
B��������Ϊ![]() ���ˣ���
���ˣ���
��ȫͼ�����£�
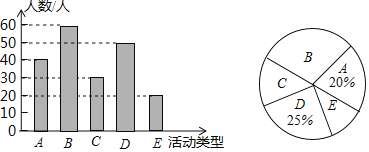
��3������ѧ��Ȥ���������������ε�Բ�ĽǵĶ���Ϊ![]() ��
��
�ʴ�Ϊ��108����
��4�����Ƹ�Уϲ��A��B��C������ѧ������![]() ���ˣ���
���ˣ���
��5������״ͼ���£�
 ��
��
����״ͼ֪������12�ֵȿ��ܽ��������һ��һŮ����8�ֽ����
��պ�һ��һŮ�μӾ����ĸ���![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������ABCD��λ����ͼ��ʾ����
�У�������ABCD��λ����ͼ��ʾ����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����������
����������![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ����������
����������![]() �����������Ĺ��ɽ�����ȥ����
�����������Ĺ��ɽ�����ȥ����![]() �������ε����Ϊ_____________��
�������ε����Ϊ_____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���E��CD����һ�㣬![]() ������AE��BE��BD����AE��BD���ڵ�F����
������AE��BE��BD����AE��BD���ڵ�F����![]() ����
����![]() ��������
��������

A.15.5B.16.5C.17.5D.18.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A����1��4����B����4��0����C����1��0����

��1����A1B1C1����ABC����ԭ��O�Գƣ�������A1B1C1��д����A1�����ꣻ
��2����A2B2C2����ABC��ԭ��O˳ʱ����ת90���õ��ģ�������A2B2C2��д����A2�����ꣻ
��3������OA��OA2������ABC��ԭ��O˳ʱ����ת90���õ�����A2B2C2�Ĺ����У������߶�OA�任��OA2������ɨ�����������Ƕ��٣���ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
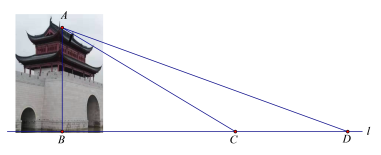
����Ŀ��ˮ����λ�ڵ��ֺӺ���ۺ�����ڣ��ǻ���ˮϵ�����ֺ��ε���������Ҫ�ı�־�Ծ��ۣ��ڿ���ʵ����У�ijУ���꼶��ѧ��ȤС�����������ˮ���ŵĸߣ����ǵIJ����������£���ͼ������D����õ�A������Ϊ20��������ˮ���ŵķ���ǰ��13����C������õ�A������Ϊ31������D��C��B��һֱ���ϣ������ˮ����AB�ĸߣ�����ȷ��0.1�ף�
���ο����ݣ�sin20���0.34��cos20���0.94��tan20���0.36��sin31���0.52��cos31���0.86��tan31���0.60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
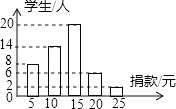
����Ŀ���ڴ���һ�վ��У�ѧУ����֧Ϊ���˽ⱾУѧ���ľ������������ȡ��50��ѧ���ľ����������ͳ�ƣ������Ƴ������ͳ��ͼ��
��1����50��ͬѧ��������Ϊ�� ��Ԫ����λ��Ϊ�� ��Ԫ��
��2������50��ͬѧ����ƽ������
��3����У����800��ѧ�����������Ƹ�Уѧ���ľ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
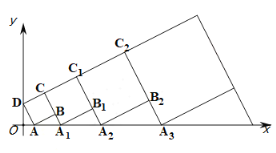
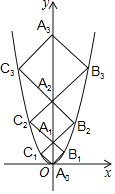
����Ŀ�����κ���y��x2��ͼ����ͼ����A0λ������ԭ�㣬��A1��A2��A3��An��y����������ϣ���B1��B2��B3��Bn�ڶ��κ���λ�ڵ�һ����ͼ���ϣ���C1��C2��C3��n�ڶ��κ���λ�ڵڶ�����ͼ���ϣ��ı���A0B1A1C1���ı���A1B2A2C2���ı���A2B3A3C3���ı���An��1BnAnn���������Σ���������An��1BnAnn���ܳ�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y1��x2+bx+c��һ�κ���y2��x+a���ڵ�A����1��0����B��d��5����
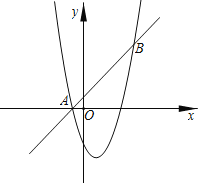
��1������κ���y1�Ľ���ʽ��
��2����y1��y2ʱ����x��ȡֵ��Χ���� ����
��3����֪��P����x���·��Ķ��κ���y1ͼ��ĵ㣬����OAP�����S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() �����߶�
�����߶�![]() �Ƶ�
�Ƶ�![]() ����ʱ�뷽����ת
����ʱ�뷽����ת![]() ���߶�
���߶�![]() .
.![]() ��
��![]() ��
��![]() ����ƽ�Ƶõ�����ֱ��
����ƽ�Ƶõ�����ֱ��![]() ����
����![]() .
.
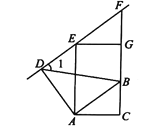
��1����![]() �Ĵ�С��
�Ĵ�С��
��2����![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com