
����Ŀ����ͼ����3��3������������ÿ��С�����εı߳���Ϊ1�������ĸ����A��B��C��D��������һ��Ϊԭ�㣬����������ֱ��Ϊ�����ᣨˮƽ��Ϊ���ᣩ������ƽ��ֱ������ϵ��ʹ�����������д������������һ��������Գƣ�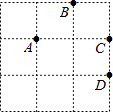
��1��ԭ����������ĸA��B��C��D ����
��2������P��3��3�������������ڵ��������ϣ������ĸ����A��B��C��D���е������ܹ������Ϊ1�ĵ���ֱ�������Σ����P������Ϊ��д�����ܵ����е�P�����꣩
���𰸡�
��1��B
��2������2,0����0,0����0,��2��
���������⣺��1�����Ե�BΪԭ��ʱ��A����1����1����C��1����1�������A�͵�C����y��Գƣ�
���Դ��ǣ�B��
��2����������ĵ�P��λ����ͼ��ʾ��
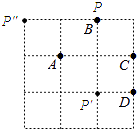
����ͼ�ο�֪��P������Ϊ����2��0����0��0����0����2����
���Դ��ǣ�����2��0����0��0����0����2����
�����㾫����������Ĺؼ�������������ȷ��λ�õ����֪ʶ�����ն���ƽ������һ��P����P�ֱ���x�ᣬy�������ߣ�����ֱ���x�ᣬy���ϣ���Ӧ����a,b�ֱ�е�P�ĺ�����������꣬�Լ��Ե��������ε��ж������⣬�˽����һ������������������ȣ���ô�����������Եı�Ҳ��ȣ���ƣ��ȽǶԵȱߣ�������ж�����������֤��ͬһ���������еı���ȣ�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ֵ��
��1����֪x�� ![]() ��1����x2��3x��1��ֵ��
��1����x2��3x��1��ֵ��
��2����֪ ![]() ����
���� ![]() ֵ��
ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С������װ��һ����ס�������ס�������װ�ι�˾��������6����ɣ��蹤Ǯ5.2��Ԫ������˾������4�ܺ�ʣ�µ����ҹ�˾����������9�ܲ�����ɣ��蹤Ǯ4.8��Ԫ����ֻѡһ����˾������ɣ��ӽ�Լ��֧�Ƕȿ��ǣ�С������ѡ��˾�������ҹ�˾����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������У����������ǵ���60���������Σ�����һ���ǵ���60���ĵ��������Σ��������Ƕ���ȵ������Σ������߶���ȵ������Σ������ǵȱ������ε����� ��
A. �٢ڢ� B. �٢ڢ� C. �٢ۢ� D. �٢ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ȵ��������ǵ�������������������������___________________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2016��Ԫ���ڼ䣬����1�����ճ�������ߴﵽ140000�˴Σ�����140000�ÿ�ѧ�������ɱ�ʾΪ�� ��
A.1.4��104
B.1.4��10��5
C.1.4��105
D.1.4��106
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����д���ʽ3��x+y��3��27��x+y����ʽ�ֽ�Ľ����ȷ���ǣ�������
A.3��x+y����x+y+3����x+y��3��
B.3��x+y��[��x+y��2��9]
C.3��x+y����x+y+3��2
D.3��x+y����x+y��3��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com