
����Ŀ����ǰ���й���ͯ��ѧ���Ҳ������ٻ�2016����ʶ�ͯ��������(IBBY)���ʰ�ͽ�������°����ץס��������ÿ��20Ԫ�ļ۸�һ�������顶��������Ʒ���������۹����з��֣�ÿ��������y�����������۵���x��Ԫ��֮��Ĺ�ϵ���±���ʾ�����ձ���y��x�Ĺ�ϵ���ɣ������������⣺

��1�������y��x�ĺ�����ϵʽ��
��2�����۵�����ʲô��Χʱ�������ӯ����
��3�������Ҫÿ�»�õ�������2000Ԫ����ô�����ÿ�µijɱ�������Ҫ����Ԫ�����ɱ�=ÿ�����ۡ���������
���𰸡���1��y��x�ĺ�����ϵʽΪ![]() ��
��
��2�����۵��۸���20Ԫ����50Ԫʱ�������ӯ����
��3����ô�����ÿ�µijɱ�������Ҫ2000Ԫ.
����������1����ÿ��������y�����۵���֮��ĺ�����ϵʽΪy=kx-b���ɴ���ϵ��������⼴�ɣ���2������������Ϊw��������=ÿ�����������������Եó�����ʽ�����ɽ���ʽ��������ʽ�����⼴�ɣ���3���ɣ�2���Ľ���ʽ��������ʽ�������⼴��.
�⣺��1����������ÿ��������![]() �����������۵���
�����������۵���![]() ��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ����� ��ѡ�����ɴ���ϵ�����ɵã�
��Ԫ��֮��Ĺ�ϵ�ɽ��ƵĿ���һ�κ����� ��ѡ�����ɴ���ϵ�����ɵã�![]()
�������������֤��
(2)����������Ϊ![]() ��Ԫ����
��Ԫ����![]()
![]()
��![]() �����
�����![]() ��
��![]() ��
��
��۵���20Ԫ��50ԪʱҲ�������
��3��������֪��![]() �����
�����![]() ��
��![]() ��
��
�ں���![]() �У���ͼ��ã���
�У���ͼ��ã���![]() ��ͼ�����£�
��ͼ�����£�
��![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
����Ҫÿ�»�õ�������2000Ԫ��![]() ��
��
���۳ɱ�![]()
��![]() ��
��![]() ��
��![]() �������������
�������������![]() ��
��![]() ��
��
������ÿ�µijɱ�������Ҫ2000Ԫ����������������ɣ�
���㾦�����⿼�������ô���ϵ���������Ľ���ʽ�����á����������������ϵ��Ӧ�á�һԪ���β���ʽ�����ã�������ɱ�������������֮��Ĺ�ϵ�ǽ���Ĺؼ���ѧ��ת����˼�룬������ת��Ϊ���̡�����ʽ����������п���������.


 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P��x��ľ�����2����y��ľ�����3���ҵ�P��y����Ҳ࣬��P��������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABMΪֱ�ǣ���CΪ�߶�BA���е㣬��D������BM�ϵ�һ�����㣨�����B�غϣ�������AD����BE��AD������ΪE������CE������E��EF��CE����BD��F�� 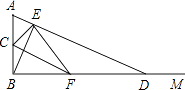
��1����֤��BF=FD��
��2����D���˶��������ܷ�ʹ���ı���ACFEΪƽ���ı��Σ��粻�ܣ���˵�����ɣ����ܣ������ʱ��A�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺ ��ɳ�������е�һ����6000Ԫ�����ס���������Ʒ����������Ʒ�ļ����ȼ���Ʒ������ ![]() ����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±�����ע������=�ۼ۩����ۣ�
����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±�����ע������=�ۼ۩����ۣ�
�� | �� | |
���ۣ�Ԫ/���� | 22 | 30 |
�ۼۣ�Ԫ/���� | 29 | 40 |
��1���ó��н���һ�ι����ļס���������Ʒȫ�������һ���ɻ�ö�������
��2���ó��еڶ����Ե�һ�εĽ����ֹ����ס���������Ʒ�����м���Ʒ�ļ������䣬����Ʒ�ļ����ǵ�һ�ε�3��������Ʒ��ԭ�����ۣ�����Ʒ�������ۣ��ڶ���������Ʒ���������Ժ��õ�������ȵ�һ�λ�õ��������180Ԫ����ڶ�������Ʒ�ǰ�ԭ�۴������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һֱ�������ε�����Ϊa��b��c����B=90�㣬��ô����x�ķ���a��x2��1����2cx+b��x2+1��=0�ĸ������Ϊ��������
A.��������ȵ�ʵ����B.����������ȵ�ʵ����
C.û��ʵ����D.��ȷ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�����ֵ��
��1����5x��3y��2xy������6x+5y��2xy��������x=��5��y=1
��2����a2b��2ab������3ab2+4ab��������a=2��b=�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ�������ѳ�Ϊ������ϲ���Ľ�������֮һ��ͨ���ֻ����Լ������ߵIJ�������Ӧ����������.�Ա��ֻ����ݷ��֣�С������![]() ����С�ղ���
����С�ղ���![]() �����ĵ�������ͬ����ÿ����
�����ĵ�������ͬ����ÿ����![]() ǧ������С�����ߵIJ�����С�ն�
ǧ������С�����ߵIJ�����С�ն�![]() ������С��ÿ����
������С��ÿ����![]() ǧ��������Ҫ���߶��ٲ���
ǧ��������Ҫ���߶��ٲ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��M=x3��3xy+2x+1��N=��3x+xy�������ʽ3M+2N�������㵱x=��1��y= ![]() ʱ��3M+2N��ֵ��
ʱ��3M+2N��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com