
【题目】如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°. 
(1)判断△ABC的形状:;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论.
【答案】
(1)等边三角形
(2)解:在PC上截取PD=AP,如图,
又∵∠APC=60°,
∴△APD是等边三角形,
∴AD=AP=PD,∠ADP=60°,即∠ADC=120°.
又∵∠APB=∠APC+∠BPC=120°,
∴∠ADC=∠APB,
在△APB和△ADC中,
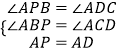 ,
,
∴△APB≌△ADC(AAS),
∴BP=CD,
又∵PD=AP,
∴CP=BP+AP.
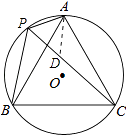
【解析】解:(1)△ABC是等边三角形. 证明如下:在⊙O中
∵∠BAC与∠CPB是 ![]() 所对的圆周角,∠ABC与∠APC是
所对的圆周角,∠ABC与∠APC是 ![]() 所对的圆周角,
所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∴△ABC为等边三角形;
所以答案是:等边三角形;
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
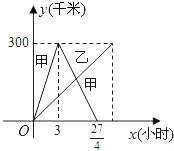
【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)在上述条件下,直接写出它们在行驶过程中相遇时的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天封塔历史悠久,是宁波著名的文化古迹.如图,从位于天封塔的观测点C测得两建筑物底部A,B的俯角分别为45°和60°,若此观测点离地面的高度为51米,A,B两点在CD的两侧,且点A,D,B在同一水平直线上,求A,B之间的距离(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,科技小组准备用材料围建一个面积为60m2的矩形科技园ABCD,其中一边AB靠墙,墙长为12 m.设AD的长为x m,DC的长为y m. 
(1)求y与x之间的函数关系式;
(2)若围成矩形科技园ABCD的三边材料总长不超过26m,材料AD和DC的长都是整米数,求出满足条件的所有围建方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育商店购进一批甲、乙两种足球,已知3个甲种足球的进价与2个乙种足球的进价的和为142元,2个甲种足球的进价与4个乙种足球的进价的和为164元.
(1)求每个甲、乙两种足球的进价分别是多少?
(2)如果购进甲种足球超过10个,超出部分可以享受7折优惠.商场决定在甲、乙两种足球选购其中一种,且数量超过10个,试帮助体育商场判断购进哪种足球省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
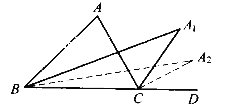
【题目】如图,在![]() ABC中,
ABC中, ![]() A=80
A=80![]() ,
, ![]() ABC与
ABC与![]() ACD的平分线交于点A1,得
ACD的平分线交于点A1,得![]() A1;
A1; ![]() A1BC与
A1BC与![]() A1CD的平分线相交于点A2,得
A1CD的平分线相交于点A2,得![]() A2;……;
A2;……; ![]() A7BC与
A7BC与![]() A7CD的平分线相交于点A8,得
A7CD的平分线相交于点A8,得![]() A8,则
A8,则![]() A8的度数为()
A8的度数为()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( ) 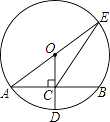
A.2 ![]()
B.8
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两种方法证明“三角形的外角和等于360°”.
已知:如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵________________________________________________________________,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°-(∠1+∠2+∠3).
∵______________,
∴∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边三角形ABC的边长为6,在AC,BC边上各取一点E,F,连接AF,BE相交于点P. 
(1)若AE=CF; ①求证:AF=BE,并求∠APB的度数;
②若AE=2,试求APAF的值;
(2)若AF=BE,当点E从点A运动到点C时,试求点P经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com