
����Ŀ��ij�����̵깺��һ���ס�������������֪3����������Ľ�����2����������Ľ��۵ĺ�Ϊ142Ԫ��2����������Ľ�����4����������Ľ��۵ĺ�Ϊ164Ԫ��
��1����ÿ���ס�����������Ľ��۷ֱ��Ƕ��٣�
��2�����������������10�����������ֿ�������7���Żݣ��̳������ڼס�����������ѡ������һ�֣�����������10�������������̳��жϹ�����������ʡǮ��
���𰸡�
��1���⣺���������Ľ�����xԪ����������Ľ�����yԪ��������ã�
![]() ��
��
��ã� ![]() ��
��
�𣺼�������Ľ�����30Ԫ����������Ľ�����26Ԫ
��2���⣺�蹺������z����z��10������������������26zԪ��������������10��30+��z��10����30��0.7Ԫ��
�ٵ�26z=10��30+��z��10����30��0.7��
���z=18��
���Ե�������������18����ѡ������һ�ּ��ɣ�
�ڵ�26z��10��30+��z��10����30��0.7��
���z��18��
���Ե���������18����ѡ��������ʡǮ��
�۵�26z��10��30+��z��10����30��0.7��
���z��18��
���Ե�������������18��������10����ѡ����������ʡǮ
����������1����ÿ����������Ľ�����xԪ��ÿ����������Ľ�����yԪ�����ݡ�3����������Ľ�����2����������Ľ��۵ĺ�Ϊ142Ԫ��2����������Ľ�����4����������Ľ��۵ĺ�Ϊ164Ԫ���г������������⣻��2���蹺������z����z��10�����ֱ��ʾ�����ֺ������������ѣ���������ʽ������⣮
�����㾫����������Ĺؼ���������һԪһ�β���ʽ���Ӧ�õ����֪ʶ������1���������⣬�ҳ����ȹ�ϵ��2���裺��δ֪����3���У��г�����ʽ�飻4���⣺�ⲻ��ʽ�飻5�����飺�Ӳ���ʽ��Ľ⼯���ҳ���������Ĵ𰸣�6����д������𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ���꼶���������࣬���μ���ѧУ���е��鷨�滭��������������ݳ����ɼ��ֱ�ѡ����10��ͬѧ�μӾ�������Щѡ�ֵľ����ɼ�(����100��)���±���ʾ��
�����ɼ�(��λ����) | |
����1�� | 80����86����88����80����88����99����80����74����91����89 |
����2�� | 85����85����87����97����85����76����88����77����87����88 |
����3�� | 82����80����78����78����81����96����97����87����92����84 |
����������⣺
(1)��������
ƽ����(��) | ����(��) | ��λ��(��) | |
������1�� | 85.5 | �� �� | 87 |
������2�� | 85.5 | 85 | �� �� |
������3�� | �� �� | 78 | 83 |
(2)�������������ͬ�ĽǶȶ������༶�ľ����ɼ�����
����ƽ�������������Ͽ�(�����ĸ��༶�ɼ���Щ)��
����ƽ��������λ�����Ͽ�(�����ĸ��༶�ɼ���Щ)��
(3)�����ÿ���༶�μӾ�����ѡ���зֱ�ѡ��3�˲μ��ܾ���������Ϊ�ĸ��༶��ʵ����ǿһЩ�����Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С�ո���ѧϰ������ʽ���ľ��飬��ͨ���ɡ����һ�㡱�ķ���̽��������θ�ʽ��������ɣ�
������С�յ�̽�����̣��벹��������
��1���������㣬���ֹ��ɣ�
����1��![]() ������2��
������2��![]() ������3��
������3��![]() ������4���� ������һ�����������������������ӣ�
������4���� ������һ�����������������������ӣ�
��2���۲졢���ɣ��ó����룮
���nΪ���������ú�n��ʽ�ӱ�ʾ���������ɣ��� ����
��3��֤�����룬ȷ�ϲ������ȷ�ԣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ���ı��ε�һ���Խ��߰��ı��ηֳ��������������Σ����ǰ������Խ��߽�����ı��εĺ�г�ߣ�����ı��ν�����г�ı��Σ������ξ��Ǻ�г�ı��Σ�
��1����ͼ1��������ABCD�У�AD��BC����BAD=120�㣬��C=75�㣬BDƽ�֡�ABC����֤��BD������ABCD�ĺ�г�ߣ�
��2����ͼ2����12��16������ͼ�ϣ�ÿ��С�����εı߳�Ϊ1����һ������BAC����A��B��C���ڸ���ϣ����ڴ������������������ͼ�ϸ���һ����D��ʹ����A��B��C��DΪ������ı��ε������Խ��߶��Ǻ�г�ߣ���������Ӧ�ĺ�г�ı��Σ�
��3���ı���ABCD�У�AB=AD=BC����BAD=90�㣬AC���ı���ABCD�ĺ�г�ߣ����BCD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ħ�г���A��ȥB�أ��ҿ�������B��ȥA�أ�ͬʱ������������ʻ�����Ե����յ��ֹͣ����ס������˼����Ϊs����λ��ǧ�ף�������ʻ��ʱ��Ϊt����λ��Сʱ����s��t֮��ĺ�����ϵ��ͼ��ʾ�������н��ۣ� �ٳ���1Сʱʱ���ס�����;��������
�ڳ���1.5Сʱʱ���ұȼ���ʻ��60ǧ�ף�
�۳���3Сʱʱ���ס���ͬʱ�����յ㣻
�ܼ��ٶ������ٶȵ�һ�룮
���У���ȷ���۵ĸ����ǣ� ��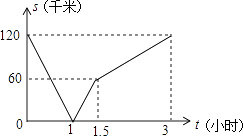
A.4
B.3
C.2
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶Ϊ1��A��P��B��C�ǡ�O�ϵ��ĸ��㣬��APC=��CPB=60�㣮 
��1���жϡ�ABC����״����
��2����̽���߶�PA��PB��PC֮���������ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ĸ���ͬ��С��������ɵ�����ͼ�ε�����ͼ������ͼ����ô�������ͼ�β������ǣ� �� 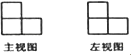
A.![]()
B.
C.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���B=40������C=60����AD��BC��D��AE����BAC��ƽ������

��1������DAE�Ķ�����
��2��д����ADΪ�ߵ�������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABC�У���A=96�����ӳ�BC��D����ABC����ACD��ƽ�����ཻ�ڵ�A1��A1BC����A1CD��ƽ�����ཻ�ڵ�A2���������ƣ���A4BC����A4CD��ƽ�����ཻ�ڵ�A5,����A5�Ķ���Ϊ�� ��
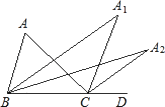
A. 19.2�� B. 8�� C. 6�� D. 3��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com