
����Ŀ����һ���ı��ε�һ���Խ��߰��ı��ηֳ��������������Σ����ǰ������Խ��߽�����ı��εĺ�г�ߣ�����ı��ν�����г�ı��Σ������ξ��Ǻ�г�ı��Σ�
��1����ͼ1��������ABCD�У�AD��BC����BAD=120�㣬��C=75�㣬BDƽ�֡�ABC����֤��BD������ABCD�ĺ�г�ߣ�
��2����ͼ2����12��16������ͼ�ϣ�ÿ��С�����εı߳�Ϊ1����һ������BAC����A��B��C���ڸ���ϣ����ڴ������������������ͼ�ϸ���һ����D��ʹ����A��B��C��DΪ������ı��ε������Խ��߶��Ǻ�г�ߣ���������Ӧ�ĺ�г�ı��Σ�
��3���ı���ABCD�У�AB=AD=BC����BAD=90�㣬AC���ı���ABCD�ĺ�г�ߣ����BCD�Ķ�����
���𰸡�
��1��
�⣺��AD��BC��
���ABC+��BAD=180�㣬��ADB=��DBC��
�ߡ�BAD=120�㣬
���ABC=60�㣮
��BDƽ�֡�ABC��
���ABD=��DBC=30�㣬
���ABD=��ADB��
���ADB�ǵ��������Σ�
�ڡ�BCD�У���C=75�㣬��DBC=30�㣬
���BDC=��C=75�㣬
���BCD����������
��BD������ABCD�ĺ�г��
��2��
�⣺��������ͼΪ��ͼ2��ͼ3
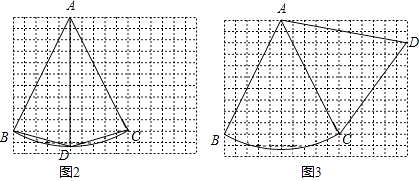
��3��
�⣺��AC���ı���ABCD�ĺ�г�ߣ�
���ACD�ǵ��������Σ�
��AB=AD=BC��
��ͼ4��
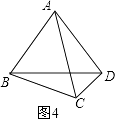
��AD=ACʱ��
��AB=AC=BC����ACD=��ADC
���ABC����������
���BAC=��BCA=60�㣮
�ߡ�BAD=90�㣬
���CAD=30�㣬
���ACD=��ADC=75�㣬
���BCD=60��+75��=135�㣮
��ͼ5��

��AD=CDʱ��
��AB=AD=BC=CD��
�ߡ�BAD=90�㣬
���ı���ABCD�������Σ�
���BCD=90��
��ͼ6��

��AC=CDʱ������C��CE��AD��E������B��BF��CE��F��
��AC=CD��CE��AD��
��AE= ![]() AD����ACE=��DCE��
AD����ACE=��DCE��
�ߡ�BAD=��AEF=��BFE=90�㣬
���ı���ABFE�Ǿ��Σ�
��BF=AE��
��AB=AD=BC��
��BF= ![]() BC��
BC��
���BCF=30�㣮
��AB=BC��
���ACB=��BAC��
��AB��CE��
���BAC=��ACE��
���ACB=��ACE= ![]() ��BCF=15�㣬
��BCF=15�㣬
���BCD=15���3=45�㣮
����������1��Ҫ֤��BD���ı���ABCD�ĺ�г�ߣ�ֻ��Ҫ֤����ABD�͡�BDC�ǵ��������ξͿ��ԣ���2���������ε����ʻ��ϵĵ㵽����ľ�����ȣ�ֻҪD�� ![]() �е�ʱ���ɵ��ı���ABDC���Ǻ�г�ı��Σ�����BC���ڡ�BAC����һ����ACΪ���ĵ���������ACD�����ɵ��ı���ABCD���Ǻ�г�ı��Σ���3����AC���ı���ABCD�ĺ�г�ߣ����Եó���ACD�ǵ��������Σ���ͼ4��ͼ5��ͼ6����������õȱ������ε����ʣ������ε����ʺ�30���ֱ�����������ʾͿ��������BCD�Ķ�����
�е�ʱ���ɵ��ı���ABDC���Ǻ�г�ı��Σ�����BC���ڡ�BAC����һ����ACΪ���ĵ���������ACD�����ɵ��ı���ABCD���Ǻ�г�ı��Σ���3����AC���ı���ABCD�ĺ�г�ߣ����Եó���ACD�ǵ��������Σ���ͼ4��ͼ5��ͼ6����������õȱ������ε����ʣ������ε����ʺ�30���ֱ�����������ʾͿ��������BCD�Ķ�����


 �ܿ�����ĩ��̾�ϵ�д�
�ܿ�����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�ڡ�ABC�У�DE��BC��DF��AC�������б���ʽ����ȷ���ǣ� �� 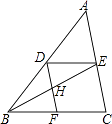
A.![]() =
= ![]()
B.![]() =
= ![]()
C.![]() =
= ![]()
D.![]() =
= ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������y=ax2��5ax+4a��x�ύ��A��B��A����B�����ࣩ��y�ύ�ڵ�C��
��1����ͼ1������AC��BC������ABC�����Ϊ3ʱ���������ߵĽ���ʽ��
��2����ͼ2����PΪ����������������һ�㣬����PC������BCP=2��ABCʱ�����P�ĺ����ꣻ
��3����ͼ3���ڣ�2���������£���F��AP�ϣ�����P��PH��x����H�㣬��K��PH���ӳ����ϣ�AK=KF����KAH=��FKH��PF=��4 ![]() a������KB���ӳ����������ڵ�Q����PQ�ij���
a������KB���ӳ����������ڵ�Q����PQ�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ʷ�ƾã��������������Ļ��ż�����ͼ����λ��������Ĺ۲��C�����������ײ�A��B�ĸ��Ƿֱ�Ϊ45���60�㣬���˹۲�������ĸ߶�Ϊ51�ף�A��B������CD�����࣬�ҵ�A��D��B��ͬһˮƽֱ���ϣ���A��B֮��ľ��루����������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ��ڵ�
��ֱ��ڵ�![]() ��
��![]() ����
����![]() ��������
��������![]() ��0������
��0������![]() ��������
��������![]() ��0����
��0����
��1����![]() ��ֵ��
��ֵ��
��2������![]() ��
��![]() ��
��![]() ���ǵڶ������ڵ�ֱ���ϵ�һ�����㣮����
���ǵڶ������ڵ�ֱ���ϵ�һ�����㣮����![]() �˶������У���д��
�˶������У���д��![]() �����
�����![]() ��
��![]() �ĺ�����ϵʽ����д���Ա���
�ĺ�����ϵʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��̽������![]() �˶���ʲôλ��ʱ��
�˶���ʲôλ��ʱ��![]() �����Ϊ
�����Ϊ![]() ����˵�����ɣ�
����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���Ƽ�С�����ò���Χ��һ�����Ϊ60m2�ľ��οƼ�ABCD������һ��AB��ǽ��ǽ��Ϊ12 m����AD�ij�Ϊx m��DC�ij�Ϊy m�� 
��1����y��x֮��ĺ�����ϵʽ��
��2����Χ�ɾ��οƼ�ABCD�����߲����ܳ�������26m������AD��DC�ij������������������������������Χ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�����̵깺��һ���ס�������������֪3����������Ľ�����2����������Ľ��۵ĺ�Ϊ142Ԫ��2����������Ľ�����4����������Ľ��۵ĺ�Ϊ164Ԫ��
��1����ÿ���ס�����������Ľ��۷ֱ��Ƕ��٣�
��2�����������������10�����������ֿ�������7���Żݣ��̳������ڼס�����������ѡ������һ�֣�����������10�������������̳��жϹ�����������ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�E������EC����AB=8��CD=2����EC�ij�Ϊ�� �� 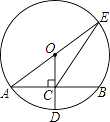
A.2 ![]()
B.8
C.2 ![]()
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽����еĿ������������ij������ȤС��ӻ�������������ȡ��������Ŀ������������Ϊ��������ͳ�ƣ���������ͼ��ʾ������ͳ��ͼ������ͳ��ͼ��������Ϣδ�������� 
�������ͼ���ṩ����Ϣ������������⣺
��1�����㱻��ȡ��������
��2���벹ȫ����ͳ��ͼ����������ͳ��ͼ�б�ʾ���š������ε�Բ�ĽǶ�����
��3������Ƹ�����һ�꣨365�죩�ﵽ���š��͡���������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com