
【题目】用两种方法证明“三角形的外角和等于360°”.
已知:如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角.
求证:∠BAE+∠CBF+∠ACD=360°.
证法1:∵________________________________________________________________,
∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,
∴∠BAE+∠CBF+∠ACD=540°-(∠1+∠2+∠3).
∵______________,
∴∠BAE+∠CBF+∠ACD=540°-180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.

【答案】见解析
【解析】
试题证法1:根据平角的定义得到∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=540°,再根据三角形内角和定理和角的和差关系即可得到结论;
证法2:要求证∠BAE+∠CBF+∠ACD=360°,根据三角形外角性质得到∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2,则∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),然后根据三角形内角和定理即可得到结论.
试题解析:证法1:∵平角等于180°,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°,∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵∠1+∠2+∠3=180°,∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
证法2:∵∠BAE=∠2+∠3,∠CBF=∠1+∠3,∠ACD=∠1+∠2,∴∠BAE+∠CBF+∠ACD=2(∠1+∠2+∠3),∵∠1+∠2+∠3=180°,∴∠BAE+∠CBF+∠ACD=360°.


科目:初中数学 来源: 题型:
【题目】下列结论正确的是( )
A.x2﹣2是二次二项式
B.单项式﹣x2的系数是1
C.使式子 ![]() 有意义的x的取值范围是x>﹣2
有意义的x的取值范围是x>﹣2
D.若分式 ![]() 的值等于0,则a=±1
的值等于0,则a=±1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°. 
(1)判断△ABC的形状:;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=40°,∠C=60°,AD⊥BC于D,AE是∠BAC的平分线.

(1)求∠DAE的度数;
(2)写出以AD为高的所有三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠B=90°,AB=6,BC=9,将△ABC折叠,使点C与AB的中点D重合,折痕交AC于点M,交BC于点N.
(1)求线段BN的长;
(2)连接CD,与MN交于点E,写出与点E相关的两个正确结论:① ;
② .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C=90°,AC=BC.作射线AP,过点B作BD⊥AP于点D,连接CD.
(1)当射线AP位于图1所示的位置时
①根据题意补全图形;
②求证:AD+BD=![]() CD.
CD.
(2)当射线AP绕点A由图1的位置顺时针旋转至∠BAC的内部,如图2,直接写出此时AD,BD,CD三条线段之间的数量关系为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
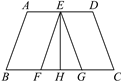
【题目】如图所示,已知AD∥BC,AB∥EF,CD∥EG,且点E在直线AD上,点F,H,G在直线BC上,EH平分∠FEG,∠A=∠D=110°,线段EH的长是不是两条平行线AD,BC之间的距离?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com