
����Ŀ��A��B�������600ǧ�ף�һ���ͳ���A�ǿ���B�ǣ�����ΪÿСʱ80ǧ�ף�ͬʱһ�������B�ǿ���A�ǣ�����Ϊ��Сʱ100ǧ�ף���ͳ���ʱ��Ϊt�� ![]()
��1����̽���� ���ͳ��������B�ǵľ���ֱ�Ϊy1��y2 �� д��y1��y2����t�ĺ�����ϵʽ�������㵱y1=200ǧ��ʱy2�Ă���
��2�������֡� ���C��A����B�ǵ��е㣬
�����ĸ������ȵ���C���ó�����C���پ�������Сʱ����һ�����ᵽ��C��
���������������100ǧ��ʱ����ʱ��t��
��3�������ߡ� ��֪�ͳ��ͳ��������A��B֮��ķ���վD����������ʱ����˿�С��ͻȻ�ӵ�����֪ͨ����Ҫ�������أ���ʱС��������ѡ��B�ǵķ�����
����һ�������������������A�Ǻ����̷���B�ǣ�������ͷʱ����Բ��ƣ���
�������������ͳ����سǣ�
��ͨ�����㣬����С��ѡ�����ַ�ʽ�ܸ��쵽��B�ǣ�
���𰸡�
��1���⣺����֪����y1=��80t+600��
��y1=0������80t+600=0�����t= ![]() ��
��
��y1=��80t+600��0��t�� ![]() ����
����
y2=100t��
��y2=600����100t=600�����t=6��
��y2=100t��0��t��6����
��y1=200ʱ����200=��80t+600�����t=5��
��t=5ʱ��y2=100��5=500��
�ʵ�y1=200ǧ��ʱy2�Ă�Ϊ500��
��2���⣺����100��60��
�����ȵ���C��
�ͳ�����C����Ҫ��ʱ�䣺600��80t1= ![]() �����t1=
�����t1= ![]() ��
��
�������C����Ҫ��ʱ�䣺100t2= ![]() �����t2=3��
�����t2=3��
![]() ��3=
��3= ![]() ��Сʱ����
��Сʱ����
���Գ������C���پ��� ![]() Сʱ���ͳ��ᵽ��C��
Сʱ���ͳ��ᵽ��C��
�����������100ǧ�ף������������
��y1��y2=100����600��80t��100t=100��
��ã�t= ![]() ��
��
��y2��y1=100����100t����600��80t��=100��
��ã�t= ![]() ��
��
���Ͽ�֪���������100ǧ��ʱ��ʱ��tΪ ![]() ��
�� ![]() Сʱ��
Сʱ��
��3���⣺������������80t+100t=600�����t= ![]() ��
��
��ʱAD=80�� ![]() =
= ![]() ��ǧ�ף���BD=600��
��ǧ�ף���BD=600�� ![]() =
= ![]() ��ǧ�ף���
��ǧ�ף���
����һ��t1=�� ![]() +600����100=
+600����100= ![]() ��Сʱ����
��Сʱ����
��������t2= ![]() ��80=
��80= ![]() ��Сʱ����
��Сʱ����
��t1��t2��
���������
��������̽��������·��=�ٶȡ�ʱ�䣬���ɵó�y1��y2����t�ĺ�����ϵʽ�����ݹ�ϵʽ���y1=200ǧ��ʱ��ʱ��t����t����y2�Ľ���ʽ�м��ɵó����ۣ����֣������ݳ�����ٶȴ��ڿͳ����ٶȿɵó�����ȵ���C�㣬���ã�1���еĺ�����ϵʽ����y=300���ɷֱ����ʱ��t1��t2 �� ��������ɵó����ۣ���2���������100ǧ�ף�������������ǣ������t��һԪһ�η��̼��ɵó����ۣ����ߣ�����ʱ��=·�̡��ٶȺͣ���������D��ʱ�䣬�ٸ���·��=�ٶȡ�ʱ�����AD��BD�ij��ȣ����ʱ��=·�̡��ٶȣ�����������ַ��������ʱ�䣬���߽��бȽϼ��ɵó����ۣ�


 С��ſ�ʱ��ҵϵ�д�
С��ſ�ʱ��ҵϵ�д� һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м����У���ȷ���ǣ� ��
A.a0=1
B.a��1=��a
C.a3a2=a5
D.2a2+3a3=5a5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
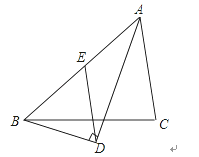
����Ŀ����ͼ������ABC�У�ADƽ����BAC��AD��BD�ڵ�D��DE��AC��AB�ڵ�E����AB=8����DE=_______
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ� С����������һ�����⣺��ͼ1���ڡ�ABC�У���D���߶�BC�ϣ���BAD=75�㣬��CAD=30�㣬AD=2��BD=2DC����AC�ij���
С�ڷ��֣�����C��CE��AB����AD���ӳ����ڵ�E��ͨ�������ACE�����������ͼ����ܹ�ʹ����õ��������ͼ 2����
��ش����ACE�Ķ�����AC�ij���
�ο�С��˼������ķ�����������⣺
��ͼ 3�����ı��� ABCD�У���BAC=90�㣬��CAD=30�㣬��ADC=75�㣬AC��BD���ڵ�E��AE=2��BE=2ED����BC�ij���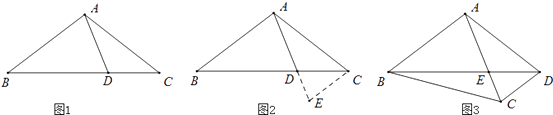
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+3��a��0����A��4��4����B��2��m�����㣬��B�������߶Գ���ľ����Ϊd������0��d��1����ʵ��m��ȡֵ��Χ�ǣ� ��
A.m��2��m��3
B.m��3��m��4
C.2��m��3
D.3��m��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���B����Ϊ��8��4����������OABC�Ƶ�O��ʱ����ת��ʹ��B����y���ϵĵ�B�䴦���õ�����OA��B��C�䣬OA����BC�ཻ�ڵ�D������D�ķ�������������ʽ�� �� 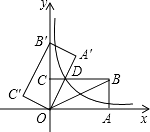
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У��ı���OABC�������Σ���A��C������ֱ�Ϊ��2��0������0��2����D��x���������ϵ�һ�㣨��D�ڵ�A���ұߣ�����BDΪ��������������BDEF��E��F�����ڵ�һ���ޣ�������FC��AB���ӳ����ڵ�G��������������![]() ��ͼ����E��G���㣬��k��ֵΪ ______________��
��ͼ����E��G���㣬��k��ֵΪ ______________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڷ���������y��![]() ������˵����ȷ���ǣ� ��
������˵����ȷ���ǣ� ��
�� �ú�����ͼ���ڵڶ��������ޣ�
�� A��x1��y1����B��x2��y2�������ڸú���ͼ���ϣ���x1��x2����y1��y2��
�� ��x��2ʱ����y����2��
�� ������������y��![]() ��һ�κ���y��x��b��ͼ�����㣬��b�ķ�Χ�ǣ�4��b��4.
��һ�κ���y��x��b��ͼ�����㣬��b�ķ�Χ�ǣ�4��b��4.
A. �� �� B. �٢� C. �ڢ� D. �ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com