
【题目】设函数y=kx2+(2k+1)x+1(k为实数)
(1)写出其中的两个特殊函数,使它们的图象不全是抛物线,并在同一直角坐标系中,用描点法画出这两个特殊函数的图象;
(2)根据所画图象,猜想出:对任意实数k,函数的图象都具有的特征,并给予证明;
(3)对任意负实数k,当x<m时,y随着x的增大而增大,试求出m的一个值.
【答案】
(1)
解:如两个函数为y=x+1,y=x2+3x+1,
函数图形如图所示

(2)
解:不论k取何值,函数y=kx2+(2k+1)x+1的图象必过定点(0,1),(﹣2,﹣1),
且与x轴至少有1个交点.证明如下:
将x=0时代入函数中解出y=1,x=﹣2时代入函数中解出y=﹣1.
所以函数的图象必过定点(0,1),(﹣2,﹣1).
又因为当k=0时,函数y=x+1的图象与x轴有一个交点;
当k≠0时,
∵△=(2k+1)2﹣4k=4k2+1>0,所以函数图象与x轴有两个交点.
所以函数y=kx2+(2k+1)x+1的图象与x轴至少有1个交点
(3)
解:只要写出m≤﹣1的数都可以.
∵k<0,
∴函数y=kx2+(2k+1)x+1的图象在对称轴直线x=﹣ ![]() 的左侧,y随x的增大而增大.
的左侧,y随x的增大而增大.
根据题意,得m≤﹣ ![]() ,而当k<0时,﹣
,而当k<0时,﹣ ![]() =﹣1﹣
=﹣1﹣ ![]() >﹣1,
>﹣1,
所以m≤﹣1
【解析】(1)令k=0或1,分别得到两个特殊函数,画出图象即可;(2)猜想:不论k取何值,函数y=kx2+(2k+1)x+1的图象必过定点(0,1),(﹣2,﹣1).由解析式变形,得y=k(x2+2x)+(x+1),可知当x2+2x=0,即x=0或﹣2时,函数值与k的取值无关,此时y=1或﹣1,可得定点坐标;(3)只求m的一个值即可.当k<0时,抛物线对称轴为直线x=﹣ ![]() ,在对称轴左侧,y随x的增大而增大,根据题意,得m≤﹣
,在对称轴左侧,y随x的增大而增大,根据题意,得m≤﹣ ![]() ,而当k<0时,﹣
,而当k<0时,﹣ ![]() =﹣1﹣
=﹣1﹣ ![]() >﹣1,可确定m的范围,在范围内取m的一个值即可.
>﹣1,可确定m的范围,在范围内取m的一个值即可.
【考点精析】利用一次函数的图象和性质和二次函数的图象对题目进行判断即可得到答案,需要熟知一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,今年三月份的电脑售价比去年同期每台降价1000元,如果卖出相同数量的电脑,去年销售额为10万元,今年销售额只有8万元.
(1)今年三月份甲种电脑每台售价多少元?
(2)为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台,有几种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF. 
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四条线段a,b,c,d如图,a:b:c:d=1:2:3:4 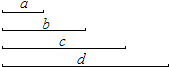
(1)选择其中的三条线段为边作一个三角形(尺规作图,要求保留作图痕迹,不必写出作法);
(2)任取三条线段,求以它们为边能作出三角形的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是 ![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2 ![]() 时,则阴影部分的面积为( )
时,则阴影部分的面积为( ) 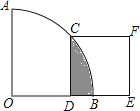
A.2π﹣4
B.4π﹣8
C.2π﹣8
D.4π﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】爱好思考的小茜在探究两条直线的位置关系查阅资料时,发现了“中垂三角形”,即两条中线互相垂直的三角形称为“中垂三角形”.如图(1)、图(2)、图(3)中,AM、BN是△ABC的中线,AN⊥BN于点P,像△ABC这样的三角形均为“中垂三角形”.设BC=a,AC=b,AB=c.
【特例探究】
(1)如图1,当tan∠PAB=1,c=4 ![]() 时,a= , b=;
时,a= , b=;
如图2,当∠PAB=30°,c=2时,a= , b=;
(2)【归纳证明】请你观察(1)中的计算结果,猜想a2、b2、c2三者之间的关系,用等式表示出来,并利用图3证明你的结论.
(3)【拓展证明】如图4,ABCD中,E、F分别是AD、BC的三等分点,且AD=3AE,BC=3BF,连接AF、BE、CE,且BE⊥CE于E,AF与BE相交点G,AD=3 ![]() ,AB=3,求AF的长.
,AB=3,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com