[题目]下列运算正确的是( )A. 4m﹣m＝3B. a3﹣a2＝aC. 2xy﹣yx＝xyD. a2b﹣ab2＝0 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】下列运算正确的是（　　）

A. 4m﹣m＝3B. a3﹣a2＝aC. 2xy﹣yx＝xyD. a2b﹣ab2＝0

【答案】C

【解析】

根据合并同类项的法则即可求出答案．

解：（A）原式＝3m，故A错误；

（B）a3﹣a2不是同类项不能合并，故B错误；

（C）原式＝2xy﹣yx＝xy，故C正确；

（D）a2b﹣ab2不是同类项不能合并，故D错误；

故选：C．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】在△ABC中，∠C=90°，BD是△ABC的角平分线，P是射线AC上任意一点（不与A、D、C三点重合），过点P作PQ⊥AB，垂足为Q，交直线BD于E．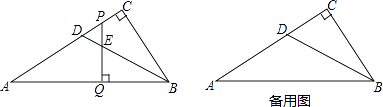
（1）如图，当点P在线段AC上时，说明∠PDE=∠PED．
（2）作∠CPQ的角平分线交直线AB于点F，则PF与BD有怎样的位置关系？画出图形并说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，点E、F分别在直线AB，CD上，点P在AB、CD之间，连结EP、FP，如图1，过FP上的点G作GH∥EP，交CD于点H，且∠1=∠2．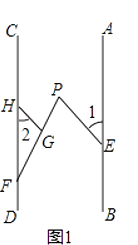

（1）求证：AB∥CD；
（2）如图2，将射线FC沿FP折叠，交PE于点J，若JK平分∠EJF，且JK∥AB，则∠BEP与∠EPF之间有何数量关系，并证明你的结论；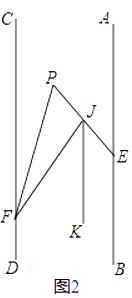

（3）如图3，将射线FC沿FP折叠，将射线EA沿EP折叠，折叠后的两射线交于点M，当EM⊥FM时，求∠EPF的度数．