
【题目】如图,在平面直角坐标系中,抛物线y=a1(x﹣2)2+2与y=a2(x﹣2)2﹣3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(﹣1,0),则△ADE与△BOC的面积比为 . 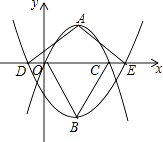
【答案】1
【解析】解:∵抛物线y=a1(x﹣2)2+2经过点(0,0),
∴0=4a1+2,
∴a1=﹣ ![]() ,
,
∴抛物线解析式为y=﹣ ![]() x2+2x,
x2+2x,
∴点C坐标(4,0),A(2,2)
∵抛物线y=a2(x﹣2)2﹣3经过点(﹣1,0),
∴0=9a2﹣3,
∴a2= ![]() ,
,
∴抛物线解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,
,
∴点E坐标(5,0),B(2,﹣3)
∴S△ADE= ![]() ×6×2=6,S△OBC=
×6×2=6,S△OBC= ![]() ×4×3=6,
×4×3=6,
∴△ADE与△BOC的面积比为为1.
所以答案是1.
【考点精析】通过灵活运用抛物线与坐标轴的交点,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.即可以解答此题.


科目:初中数学 来源: 题型:
【题目】给下列证明过程填写理由.
如图,CD⊥AB于D,点F是BC上任意一点,EF⊥AB于E,∠1=∠2,求证:∠ACB=∠3.
请阅读下面解答过程,并补全所有内容.
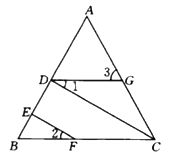
解:∵CD⊥AB,EF⊥AB(已知)
∴∠BEF=∠BDC=90°( )
∴EF∥DC( )
∴∠2=________( )
又∵∠2=∠1(已知)
∴∠1=_______(等量代换)
∴DG∥BC( )
∴∠3=________( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在8×8的正方形网格中,△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上.请你在图中找出一点D(仅一个点即可),连结DE,DF,使△DEF与△ABC全等,并给予证明.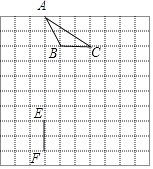
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
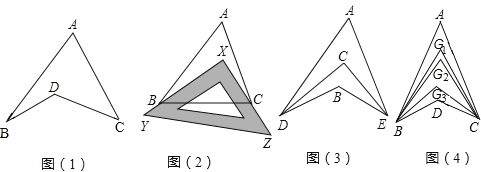
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,点P是平行四边形ABCD对角线AC、BD的交点,若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4则S1、S2、S3、S4的关系为S1=S2=S3=S4.请你说明理由;
(2)变式1:如图2,点P是平行四边形ABCD内一点,连接PA、PB、PC、PD.若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,写出S1、S2、S3、S4的关系式;
(3)变式2:如图3,点P是四边形ABCD对角线AC、BD的交点若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,写出S1、S2、S3、S4的关系式.请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为( )
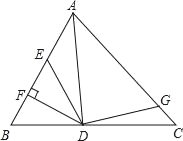
A. 12 B. 6 C. 7 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com