
【题目】给下列证明过程填写理由.
如图,CD⊥AB于D,点F是BC上任意一点,EF⊥AB于E,∠1=∠2,求证:∠ACB=∠3.
请阅读下面解答过程,并补全所有内容.
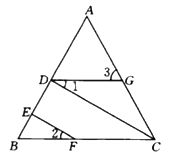
解:∵CD⊥AB,EF⊥AB(已知)
∴∠BEF=∠BDC=90°( )
∴EF∥DC( )
∴∠2=________( )
又∵∠2=∠1(已知)
∴∠1=_______(等量代换)
∴DG∥BC( )
∴∠3=________( )
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】在一次试验中,小明把一根弹簧的上端固定,在其下端悬挂物体,测得弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间的关系如下表:
之间的关系如下表:
所挂物体质量 | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧的长度 | 8 | 10 | 12 | 14 | 16 | 18 |
下列说法错误的是( )
A.弹簧的长度随所挂物体质量的变化而变化,所挂物体质量是自变量,弹簧长度是因变量
B.不挂物体时,弹簧的长度为![]()
C.弹簧的长度![]() 与所挂物体的质量
与所挂物体的质量![]() 之间的关系式是
之间的关系式是![]()
D.在弹性限度内,当所挂物体的质量为![]() 时,弹簧的长度为
时,弹簧的长度为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为 . 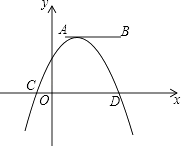
查看答案和解析>>
科目:初中数学 来源: 题型:
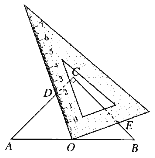
【题目】如图,在等腰直角△ABC中,∠C=90°,点O是AB的中点,边AC的长为![]() ,将一块边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的一条直角边与 AC相交,交点为点D,另一条直角边与BC相交,交点为点E.证明:等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值
,将一块边长足够大的三角板的直角顶点放在点O处,将三角板绕点O旋转,始终保持三角板的一条直角边与 AC相交,交点为点D,另一条直角边与BC相交,交点为点E.证明:等腰直角三角形ABC的边被三角板覆盖部分的两条线段CD与CE长度之和为定值![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′,利用网格点画图和无刻度的直尺画图并解答(保留画图痕迹):
(1)画出△A′B′C′;
(2)画出△ABC的高,即线段BD;
(3)连接AA′、 CC′,那么AA′与CC′的关系是________;线段AC扫过图形的面积为____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=a1(x﹣2)2+2与y=a2(x﹣2)2﹣3的顶点分别为A,B,与x轴分别交于点O,C,D,E.若点D的坐标为(﹣1,0),则△ADE与△BOC的面积比为 . 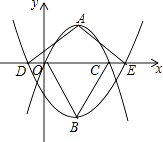
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等腰直角三角形,∠ABC=90°,AB=BC,点A在x轴的负半轴上,点B是y轴上的一个动点,点C在点B的上方,
(1)如图1当点A的坐标为(﹣3,0),点B的坐标为(0,1)时,求点C的坐标;
(2)设点A的坐标为(a,0),点B的坐标为(0,b).过点C作CD⊥y轴于点D,在点B运动过程中(不包含△ABC的一边与坐标轴重合的情况),猜想线段OD的长与a、b的数量关系,并说明理由;
(3)在(2)的条件下如图4,当x轴平分∠BAC时,BC交x轴于点E,过点作CF⊥x轴于点F.说明此时线段CF与AE的数量关系(用含a、b的式子表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com