
【题目】如图,△ABC为等腰直角三角形,∠ABC=90°,AB=BC,点A在x轴的负半轴上,点B是y轴上的一个动点,点C在点B的上方,
(1)如图1当点A的坐标为(﹣3,0),点B的坐标为(0,1)时,求点C的坐标;
(2)设点A的坐标为(a,0),点B的坐标为(0,b).过点C作CD⊥y轴于点D,在点B运动过程中(不包含△ABC的一边与坐标轴重合的情况),猜想线段OD的长与a、b的数量关系,并说明理由;
(3)在(2)的条件下如图4,当x轴平分∠BAC时,BC交x轴于点E,过点作CF⊥x轴于点F.说明此时线段CF与AE的数量关系(用含a、b的式子表示).

【答案】(1)C(﹣1,4);(2)OD=a﹣b;(3)aAE+bCF=﹣a(a+b).
【解析】
(1)先确定出OA=3,OB=1,进而判断出△AOB≌△BDC,即可得出BD=3,CD=1,即可得出结论;
(2)分三种情况,同(1)的方法即可得出结论;
(3)先确定出OF=CD=﹣b,CF=OD=b﹣a,进而得出AF=OA+OF=﹣a﹣b,在判断出△AOB∽△CFE,即可得出EF=![]() (b﹣a),进而得出AE=AF﹣EF=﹣a﹣b﹣
(b﹣a),进而得出AE=AF﹣EF=﹣a﹣b﹣![]() (b﹣a),即可得出结论.
(b﹣a),即可得出结论.
解:(1)如图1,
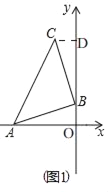
∵点A的坐标为(﹣3,0),点B的坐标为(0,1),
∴OA=3,OB=1,
过点C作CD⊥y轴于D,
∴∠BCD+∠CBD=90°,
∵∠ABC=90°,
∴∠CBD+∠ABO=90°,
∴∠ABO=∠BCD,
在△AOB和△BDC中,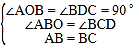 ,
,
∴△AOB≌△BDC,
∴BD=OA=3,CD=OB=1,
∴OD=OB+BD=4,
∴C(﹣1,4);
(2)当点B在y轴正半轴上时,
如图1,∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=b,
∴OD=OB+BD=b+(﹣a)=b﹣a,
当点B在y轴负半轴上,点C在第一象限时,如图2,
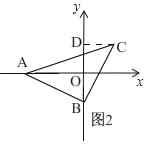
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=BD﹣OB=(﹣a)﹣(﹣b)=b﹣a,
当点B在y轴负半轴,点C在第四象限时,如图3,
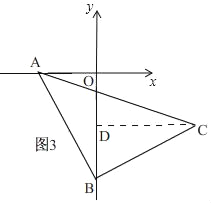
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,
由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=OB﹣BD=﹣b﹣(﹣a)=a﹣b;
(3)如图4,
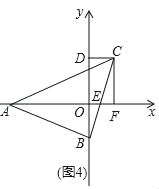
∵点A的坐标为(a,0),点B的坐标为(0,b),
∴OA=|a|=﹣a,OB=|b|=﹣b,由(1)知,△AOB≌△BDC,
∴BD=OA=﹣a,CD=OB=﹣b,
∴OD=BD﹣OB=(﹣a)﹣(﹣b)=b﹣a,
∵CF⊥OA于F,
∴四边形ODCF是矩形,
∴OF=CD=﹣b,CF=OD=b﹣a,
∴AF=OA+OF=﹣a﹣b,
∵△ABC是等腰直角三角形,
∴∠BAC=45°,
∵AF平分∠BAC,
∴∠OAC=∠OAB=22.5°,
∴∠ECF=∠ACF﹣∠ACB=90°﹣∠OAC﹣∠ACB=22.5°=∠OAB,
∵∠AOB=∠CFE,
∴△AOB∽△CFE,
∴![]() ,
,
∴![]() ,
,
∴EF=![]() (b﹣a),
(b﹣a),
∴AE=AF﹣EF=﹣a﹣b﹣![]() (b﹣a),
(b﹣a),
∵CF=b﹣a,
∴AE=﹣a﹣b﹣![]() CF,
CF,
∴aAE+bCF=﹣a(a+b).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】给下列证明过程填写理由.
如图,CD⊥AB于D,点F是BC上任意一点,EF⊥AB于E,∠1=∠2,求证:∠ACB=∠3.
请阅读下面解答过程,并补全所有内容.
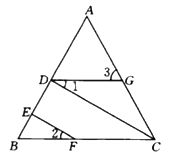
解:∵CD⊥AB,EF⊥AB(已知)
∴∠BEF=∠BDC=90°( )
∴EF∥DC( )
∴∠2=________( )
又∵∠2=∠1(已知)
∴∠1=_______(等量代换)
∴DG∥BC( )
∴∠3=________( )
查看答案和解析>>
科目:初中数学 来源: 题型:
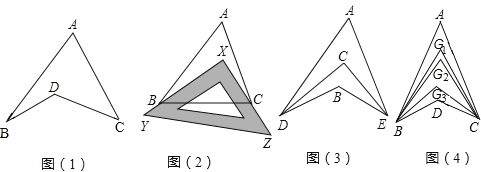
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品﹣﹣圆规.我们不妨把这样图形叫做“规形图”.
(1)观察“规形图”,试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,∠A=40°,则∠ABX+∠ACX= °;
②如图3,DC平分∠ADB,EC平分∠AEB,若∠DAE=40°,∠DBE=130°,求∠DCE的度数;
③如图4,∠ABD,∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=133°,∠BG1C=70°,求∠A的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,点P是平行四边形ABCD对角线AC、BD的交点,若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4则S1、S2、S3、S4的关系为S1=S2=S3=S4.请你说明理由;
(2)变式1:如图2,点P是平行四边形ABCD内一点,连接PA、PB、PC、PD.若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,写出S1、S2、S3、S4的关系式;
(3)变式2:如图3,点P是四边形ABCD对角线AC、BD的交点若S△PAB=S1,S△PBC=S2,S△PCD=S3,S△PAD=S4,写出S1、S2、S3、S4的关系式.请你说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=______s时,以A、C、E、F为顶点四边形是平行四边形.
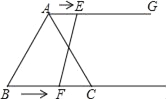
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年10月份某商场用19600元同时购进A、B两种新型节能日光灯共440盏,A型日光灯每盏进价为40元,售价为60元,B型日光灯每盏进价为50元,售价为80元.
(1)求10月份两种新型节能日光灯各购进多少盏?
(2)将10月份购买的日光灯从生产基地运往商场的过程中,A型日光灯出现![]() 的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润
的损坏,B型日光灯完好无损,商场决定对A、B两种日光灯的售价进行调整,使这批日光灯全部售完后,商场可获得10664元的利润![]() 型日光灯在原售价基础上提高
型日光灯在原售价基础上提高![]() ,问A型日光灯调整后的售价为多少元?
,问A型日光灯调整后的售价为多少元?
(3)进入11月份,B型日光灯的需求量增大,于是商场在筹备“双十一”促销活动时,决定去甲、乙两个生产基地只购进一批B型日光灯,甲、乙生产基地给出了不同的优惠措施:
甲生产基地:B型日光灯出厂价为每盏50元,折扣如表一所示
乙生产基地:B型日光灯出厂价为每盏47元,同时当出厂总金额达一定数量后还可按表二返现金.
表一
甲生产基地 | |
一次性购买的数量 | 折扣数 |
不超过150盏的部分 |
|
超过150盏的部分 | 9折 |
表二
乙生产基地 | |
出厂总金额 | 返现金 |
不超过5640元 | 0元 |
超过5640元,但不超过9353元 | 返现300元 |
超过9353元 | 先返现出厂总金额的 |
已知该商场在甲生产基地购买B型日光灯共支付7350元,在乙生产基地购买B型日光灯共支付9006元,若将在两个生产基地购买的B型日光灯的总量改由在乙生产基地一次性购买,则支付总金额比在甲、乙两生产基地分别购买的支付金额之和可节约多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解初三女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.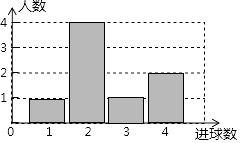
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有初三女生400人,从中任选一位女生,求选到的女生投篮成绩为“优秀”等级的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为40和28,则△EDF的面积为( )
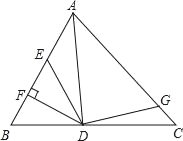
A. 12 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
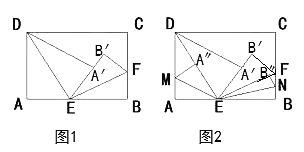
【题目】如图1,长方形ABCD沿着直线DE和EF折叠,使得AB的对应点![]() 和点E在同一条直线上。
和点E在同一条直线上。
(1)求∠DEF的度数;
(2)如图2,若再次沿着直线EM和EN折叠使得A、B的对应点![]() 分别落在DE和EF上,∠AEM=34°,求∠BEN的度数。
分别落在DE和EF上,∠AEM=34°,求∠BEN的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com