练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】因式分解：2a2﹣8= ．

    【答案】2（a+2）（a﹣2）
    【解析】解：2a2﹣8=2（a2﹣4）=2（a+2）（a﹣2）． 故答案为：2（a+2）（a﹣2）．
    首先提取公因式2，进而利用平方差公式分解因式即可．此题主要考查了提取公因式法以及公式法分解因式，熟练应用乘法公式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，已知点A、B的坐标分别为（8，0）、（0，），C是AB的中点，过点C作y轴的垂线，垂足为D，动点P从点D出发，沿DC向点C匀速运动，过点P作x轴的垂线，垂足为E，连接BP、EC．当BP所在直线与EC所在直线第一次垂直时，点P的坐标为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AC和BD相交于O点，若OA=OD，用“SAS”证明△AOB≌△DOC还需（ ）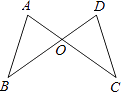
    A.AB=DC
    B.OB=OC
    C.∠C=∠D
    D.∠AOB=∠DOC

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一组数据5，4，2，5，6的中位数是（　　）
    A.5
    B.4
    C.2
    D.6

    查看答案和解析>>

    科目：初中数学 来源： 题型：

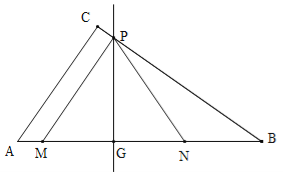
    【题目】如图，在Rt△ABC中，∠ACB＝900，AC=6，BC=8．动点M从点A出发，以每秒1个单位长度的速度沿AB向点B匀速运动；同时，动点N从点B出发，以每秒3个单位长度的速度沿BA向点A匀速运动．过线段MN的中点G作边AB的垂线，垂足为点G，交△ABC的另一边于点P，连接PM、PN，当点N运动到点A时，M、N两点同时停止运动，设运动时间为t秒．

    （1）当t＝ 秒时，动点M、N相遇；

    （2）设△PMN的面积为S，求S与t之间的函数关系式；

    （3）取线段PM的中点K，连接KA、KC，在整个运动过程中，△KAC的面积是否变化？若变化，直接写出它的最大值和最小值；若不变化，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】红枣丰收了，为了运输方便，小华的爸爸打算把一个长为（a+2b）cm、宽为（a+b）cm的长方形纸板制成一个有底无盖的盒子，在长方形纸板的四个角各截去一个边长为 bcm的小正方形，然后沿折线折起即可，如图所示，现将盒子的外表面贴上彩色花板．
    （1）则至少需要彩纸的面积是多少？
    （2）当a=8，b=6时，求至少需要彩纸的面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知|a|＝5，b2＝4，且a<b，求ab－(a＋b)的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BC=5cm，BP、CP分别是∠ABC和∠ACB的角平分线，且PD∥AB，PE∥AC，则△PDE的周长是cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，△ABC和△DEF中，AB=AC，DE=DF，∠A=∠D．

    （1）求证：；

    （2）由（1）中的结论可知，等腰三角形ABC中，当顶角∠A的大小确定时，它的对边（即底边BC）与邻边（即腰AB或AC）的比值也就确定，我们把这个比值记作T（A），即T（A）==，如T（60°）=1．

    ①理解巩固：T（90°）= ，T（120°）= ，若α是等腰三角形的顶角，则T（α）的取值范围是 ；

    ②学以致用：如图2，圆锥的母线长为9，底面直径PQ=8，一只蚂蚁从点P沿着圆锥的侧面爬行到点Q，求蚂蚁爬行的最短路径长（精确到0.1）．

    （参考数据：T（160°）≈1.97，T（80°）≈1.29，T（40°）≈0.68）

    查看答案和解析>>

    同步练习册答案