Question

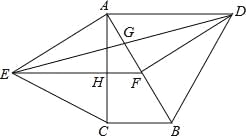
【题目】如图，分别以直角△ABC的斜边AB，直角边AC为边向△ABC外作等边△ABD和等边△ACE，F为AB的中点，DE与AB交于点G，EF与AC交于点H，∠ACB=90°，∠BAC=30°．给出如下结论：

①EF⊥AC；②四边形ADFE为菱形；③AD=4AG；④FH=BD；其中正确结论的是（ ）

A. ①②③ B. ①②④ C. ①③④ D. ②③④

Answer 1

【答案】C

【解析】试题分析：∵△ACE是等边三角形，

∴∠EAC=60°，AE=AC，

∵∠BAC=30°，

∴∠FAE=∠ACB=90°，AB=2BC，

∵F为AB的中点，

∴AB=2AF，

∴BC=AF，

∴△ABC≌△EFA，

∴FE=AB，

∴∠AEF=∠BAC=30°，

∴EF⊥AC，故①正确，

∵EF⊥AC，∠ACB=90°，

∴HF∥BC，

∵F是AB的中点，

∴HF=BC，

∵BC=AB，AB=BD，

∴HF=BD，故④说法正确；

∵AD=BD，BF=AF，

∴∠DFB=90°，∠BDF=30°，

∵∠FAE=∠BAC+∠CAE=90°，

∴∠DFB=∠EAF，

∵EF⊥AC，

∴∠AEF=30°，

∴∠BDF=∠AEF，

∴△DBF≌△EFA（AAS），

∴AE=DF，

∵FE=AB，

∴四边形ADFE为平行四边形，

∵AE≠EF，

∴四边形ADFE不是菱形；

故②说法不正确；

∴AG=AF，

∴AG=AB，

∵AD=AB，

则AD=4AG，故③说法正确，

故选：C．