
【题目】某电视机厂生产甲、乙、丙三种不同型号的电视机,出厂价分别为1200元,2000元,2200元.某商场同时从该厂购进其中两种不同型号的电视机共50台,正好用去80000元.
(1)该商场有几种进货方案?(写出演算步骤)
(2)若该商场销售甲、乙、丙种电视机每台可分别获利200元,250元,300元,如何进货可使销售时获利最大?最大利润是多少?
【答案】(1)有两种进货方案,方案一:购买25台甲型电视和25台乙型电视;方案二:购买30台甲型和20台丙型电视;(2)按方案二:购买30台甲型电视和20台丙型电视进货,可获利最大,最大利润为12000元.
【解析】(1)设购进甲型电视机x台,乙型电视机y台,丙型电视机z台,分①只购进甲、乙两种不同型号的电视机、②只购进甲、丙两种不同型号的电视机、③只购进乙、丙两种不同型号的电视机三种情况考虑,根据三种型号电视机的出厂价、购进台数以及购机的总花费为80000元即可得出二元一次方程组,解方程组后再根据x、y、z均为正整数即可得出结论;
(2)根据总利润=每台利润×购进台数即可求出各购机方案的利润,比较后即可得出结论.
解:(1) 设甲、乙、丙三种型号的电视机分别购买x、y、z台.
若购进甲、乙两种型号的电视机,则
![]()
解之得,![]()
若购进甲、丙两种型号的电视机,则
![]()
解之得,![]()
若购进乙、丙两种型号的电视机,则
![]()
解之得,![]() (舍)
(舍)
故该商场有两种进货方案,即
方案一:购买25台甲型电视和25台乙型电视;
方案二:购买30台甲型电视和20台丙型电视
(2)若按方案一进货,利润为![]() (元)
(元)
若按方案二进货,利润为![]() (元)
(元)
∵![]()
∴按方案二:购买30台甲型电视和20台丙型电视进货,可获利最大
最大利润为12000元.


科目:初中数学 来源: 题型:
【题目】某单位急需用车,但不准备买车,他们准备和一个体车主或一国营出租车公司中的一家签订合同,设汽车每月行驶x km,应付给个体车主的月租费是![]() 元,应付给国营出租车公司的月租费是
元,应付给国营出租车公司的月租费是![]() 元,
元, ![]() ,
, ![]() 分别与
分别与![]() 之间的函数关系的图象(两条射线)如图所示,观察图象,回答下列问题.
之间的函数关系的图象(两条射线)如图所示,观察图象,回答下列问题.
(1)分别写出![]() ,
, ![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)每月行驶的路程在什么范围内时,租国营公司的车合算?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
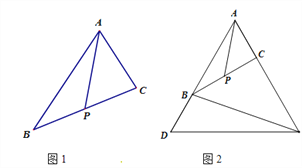
问题:如图1,在△![]() 中,点
中,点![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() <
<![]() 小明提供了他研究这个问题的思路:从点
小明提供了他研究这个问题的思路:从点![]() 为
为![]() 的中点出发,可以构造以
的中点出发,可以构造以![]() 、
、![]() 为邻边的平行四边形
为邻边的平行四边形![]() ,结合平行四边形的性质以及三角形两边之和大于第三边的性质便可解决这个问题.请结合小明研究问题的思路,解决下列问题:
,结合平行四边形的性质以及三角形两边之和大于第三边的性质便可解决这个问题.请结合小明研究问题的思路,解决下列问题:
(1)完成上面问题的解答;
(2)如果在图1中,∠![]() =60°,延长
=60°,延长![]() 到
到![]() ,使得
,使得![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() ,连结
,连结![]() ,如图2. 请猜想线段
,如图2. 请猜想线段![]() 与线段
与线段![]() 之间的数量关系.并加以证明.
之间的数量关系.并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,若△ABC在第一象限,则△ABC关于x轴对称的图形所在的位置是( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
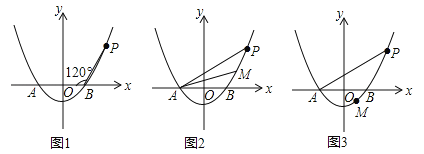
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为![]() ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD;其中正确结论的是( )
BD;其中正确结论的是( )

A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题
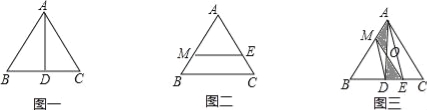
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE.
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com