
【题目】问题探究:
1.新知学习
若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”,其“面线”被该平面图形截得的线段叫做该平面图形的“面径”(例如圆的直径就是圆的“面径”).
2.解决问题
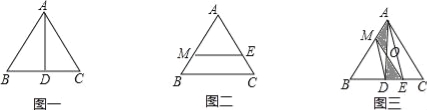
已知等边三角形ABC的边长为2.
(1)如图一,若AD⊥BC,垂足为D,试说明AD是△ABC的一条面径,并求AD的长;
(2)如图二,若ME∥BC,且ME是△ABC的一条面径,求面径ME的长;
(3)如图三,已知D为BC的中点,连接AD,M为AB上的一点(0<AM<1),E是DC上的一点,连接ME,ME与AD交于点O,且S△MOA=S△DOE.
①求证:ME是△ABC的面径;
②连接AE,求证:MD∥AE;
(4)请你猜测等边三角形ABC的面径长l的取值范围(直接写出结果)
【答案】(1)AD=![]() ;(2)ME=
;(2)ME=![]() ;(3)详见解析;(3)
;(3)详见解析;(3)![]() ≤l≤
≤l≤![]() .
.
【解析】
试题分析:(1)根据等腰三角形三线合一即可证明,利用直角三角形30°性质,即可求出AD.(2)根据相似三角形性质面积比等于相似比的平方,即可解决问题.(3)如图三中,作MN⊥AE于N,DF⊥AE于F,先证明MN=DF,推出四边形MNFD是平行四边形即可.
(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,求出EM,利用不等式性质证明ME≥![]() 即可解决问题.
即可解决问题.
试题解析:(1)如图一中,
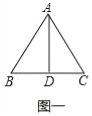
∵AB=AC=BC=2,AD⊥BC,
∴BD=DC,
∴S△ABD=S△ADC,
∴线段AD是△ABC的面径.
∵∠B=60°,
∴sin60°=![]() ,
,
∴![]() ,
,
∴AD=![]() .
.
(2)如图二中,
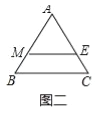
∵ME∥BC,且ME是△ABC的一条面径,
∴△AME∽△ABC,![]() =
=![]() ,
,
∴![]() ,
,
∴ME=![]() .
.
(3)如图三中,作MN⊥AE于N,DF⊥AE于F.
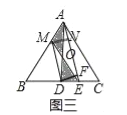
∵S△MOA=S△DOE,
∴S△AEM=S△AED,
∴![]() AEMN=
AEMN=![]() AEDF,
AEDF,
∴MN=DF,
∵MN∥DF,
∴四边形MNFD是平行四边形,
∴DM∥AE.
(4)如图四中,作MF⊥BC于F,设BM=x,BE=y,
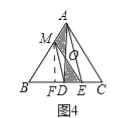
∵DM∥AE,
∴![]() ,
,
∴![]() ,
,
∴xy=2,
在RT△MBF中,∵∠MFB=90°,∠B=60°,BM=x,
∴BF=![]() x,MF=
x,MF=![]() x,
x,
∴ME=![]()
∴ME≥![]() ,
,
∵ME是等边三角形面径,AD也是等边三角形面积径,
∴等边三角形ABC的面径长l的取值范围![]() ≤l≤
≤l≤![]() .
.


科目:初中数学 来源: 题型:
【题目】某电视机厂生产甲、乙、丙三种不同型号的电视机,出厂价分别为1200元,2000元,2200元.某商场同时从该厂购进其中两种不同型号的电视机共50台,正好用去80000元.
(1)该商场有几种进货方案?(写出演算步骤)
(2)若该商场销售甲、乙、丙种电视机每台可分别获利200元,250元,300元,如何进货可使销售时获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在一次扶贫助残活动中,共捐款5280000元,将5280000用科学记数法表示为( )
A. 5.28×106 B. 5.28×107
C. 52.8×106 D. 0.528×107
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(8×106)(5×102)(2×10)=M×10a , 则M , a的值为( )
A.M=8,a=8
B.M=2,a=9
C.M=8,a=10
D.M=5,a=10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点P位于x轴上方,到x轴的距离为2,到y轴的距离为5,则点P坐标为( )
A. (2,5)B. (5,2)C. (2,5)或(-2,5)D. (5,2)或(-5,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
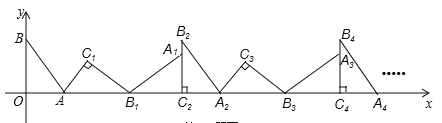
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】想表示某种品牌奶粉中蛋白质、钙、维生素、糖、其它物质的含量的百分比,应该利用( )
A. 条形统计图 B. 扇形统计图 C. 折线统计图 D. 以上都可以
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com