
【题目】如图,已知△ABC,按如下步骤作图: 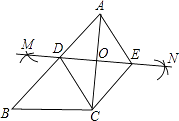
①分别以A、C为圆心,以大于 ![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形;
(2)当∠ACB=90°,BC=6,△ADC的周长为18时,求四边形ADCE的面积.
【答案】
(1)证明:由题意可知:
∵分别以A、C为圆心,以大于 ![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
∴直线DE是线段AC的垂直平分线,
∴AC⊥DE,即∠AOD=∠COE=90°;
且AD=CD、AO=CO,
又∵CE∥AB,
∴∠1=∠2,
在△AOD和△COE中
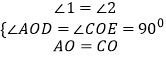 ,
,
∴△AOD≌△COE(AAS),
∴OD=OE,
∵A0=CO,DO=EO,
∴四边形ADCE是平行四边形,
又∵AC⊥DE,
∴四边形ADCE是菱形
(2)解:当∠ACB=90°时,
OD∥BC,
即有△ADO∽△ABC,
∴ ![]() ,
,
又∵BC=6,
∴OD=3,
又∵△ADC的周长为18,
∴AD+AO=9,
即AD=9﹣AO,
∴OD= ![]() =3,
=3,
可得AO=4,
∴DE=6,AC=8,
∴S= ![]() ACDE=
ACDE= ![]() ×8×6=24
×8×6=24
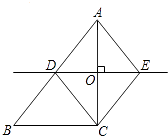
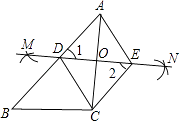
【解析】(1)利用直线DE是线段AC的垂直平分线,得出AC⊥DE,即∠AOD=∠COE=90°,进而得出△AOD≌△COE,即可得出四边形ADCE是菱形;(2)利用当∠ACB=90°时,OD∥BC,即有△ADO∽△ABC,即可得出AC和DE的长即可得出四边形ADCE的面积.
【考点精析】掌握线段垂直平分线的性质和勾股定理的概念是解答本题的根本,需要知道垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】用频数分布直方图描述数据,下列说法正确的是( )
A. 所分的组数与数据的个数无关
B. 长方形的高越高,说明落在这个区域的数据越多
C. 可以不求最大值和最小值的差
D. 可以看出数据的变化趋势
查看答案和解析>>
科目:初中数学 来源: 题型:
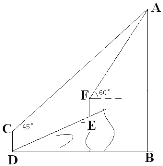
【题目】如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC。
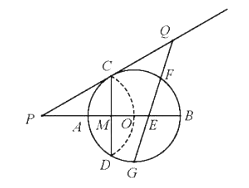
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合)。问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
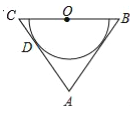
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.

第21题图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com