
【题目】
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.

第21题图
科目:初中数学 来源: 题型:
【题目】下列事件中,属于必然事件的是( )
A. 打开电视机正在播放广告B. 投掷一枚质地均匀的硬币100次,正面向上的次数为50次
C. 任意画一个三角形,其内角和为180°D. 任意一个二次函数图象与x轴有交点
查看答案和解析>>
科目:初中数学 来源: 题型:
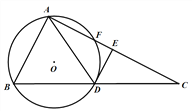
【题目】如图.点D是Rt△ABC斜边BC的中点,⊙O是△ABD的外接圆,交AC于点F. DE平分∠ADC,交AC于点E.
求证:DE是⊙O的切线;
若CE=4,DE=2,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图: 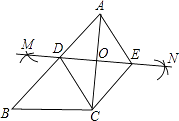
①分别以A、C为圆心,以大于 ![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形;
(2)当∠ACB=90°,BC=6,△ADC的周长为18时,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N. 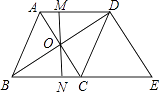
(1)请你判断OM和ON的数量关系,并说明理由;
(2)过点D作DE∥AC交BC的延长线于点E,当AB=6,AC=8时,求△BDE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)(﹣4a2bc3)2 ![]() a(b2c)2(﹣abc2)4
a(b2c)2(﹣abc2)4
(2)先化简,再求值(3a+2b)(2a﹣3b)﹣(a﹣2b)(2a﹣b),其中a= ![]() ,b=
,b= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有2位股东,20名工人、从2006年至2008年,公司每年股东的总利润和每年工人的工资总额如图所示. 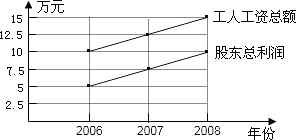
(1)填写下表:
年份 | 2006年 | 2007年 | 2008年 |
工人的平均工资/元 | 5000 | ||
股东的平均利润/元 | 25000 |
(2)假设在以后的若干年中,每年工人的工资和股东的利润都按上图中的速度增长,那么到哪一年,股东的平均利润是工人的平均工资的8倍?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com