
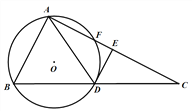
【题目】如图.点D是Rt△ABC斜边BC的中点,⊙O是△ABD的外接圆,交AC于点F. DE平分∠ADC,交AC于点E.
求证:DE是⊙O的切线;
若CE=4,DE=2,求⊙O的直径.
【答案】(1)证明见解析;(2)5
【解析】(1)连接BF,OD,利用三角形中位线定理证明OD∥AC,再证明OD⊥DE即可.
(2)先证FD垂直平分BC ,再由Rt△DFE∽Rt△CDE求出FE.
解:(1)连接BF,OD

∵∠BAC=90°
∴BF为直径,O为BF中点.
∵点D是BC的中点
∴OD是△BFC的中位线,即OD∥AC.
∵点D是Rt△ABC斜边BC的中点
∴△ADC是等腰三角形
∵DE平分∠ADC
∴DE⊥AC
∴OD⊥DE,即DE是⊙O的切线
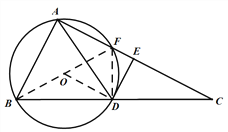
(2)连接DF.
∵BF为直径
∴FD⊥BC
又∵点D是BC的中点
∴FD垂直平分BC 即BF=FC
由Rt△DFE∽Rt△CDE
![]() 即
即![]() . FE=1
. FE=1
∴BF=FC=FE+EC=5
“点睛”考查了切线的判定定理,涉及的知识有,全等三角形的判定与性质,平行线的判定与性质,以及圆内接四边形的性质,切线的判定方法有两种:有点连接证垂直;无点作垂线,证明垂线段等于半径.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
的图象与一次函数y=kx+b的图象交于A,B两点,点A的坐标为(2,6),点B的坐标为(n,1).
(1)求反比例函数与一次函数的表达式;
(2)点E为y轴上一个动点,若S△AEB=5,求点E的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用频数分布直方图描述数据,下列说法正确的是( )
A. 所分的组数与数据的个数无关
B. 长方形的高越高,说明落在这个区域的数据越多
C. 可以不求最大值和最小值的差
D. 可以看出数据的变化趋势
查看答案和解析>>
科目:初中数学 来源: 题型:
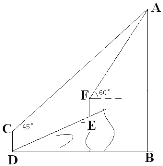
【题目】如图,在一次数学课外实践活动中,要求测量山坡前某建筑物的高度AB.小刚在D处用高1.5m的测角仪CD,测得该建筑物顶端A的仰角为45°,然后沿倾斜角为30°的山坡向上前进20m到达E,重新安装好测角仪后又测得该建筑物顶端A的仰角为60°.求该建筑物的高度AB.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,AB为直径,CD为弦,AB与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,链接PC。
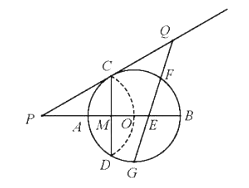
(1)求CD的长;
(2)求证:PC是⊙O的切线;
(3)点G为弧ADB的中点,在PC延长线上有一动点Q,连接QG交AB于点E,交弧BC于点F(F与B、C不重合)。问GEGF是否为定值?如果是,求出该定值;如果不是,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
如图,点B,F,C,E在直线l上(F,C之间不能直接测量),点A,D在l异侧,测得AB=DE,AC=DF,BF=EC.
(1)求证:△ABC≌△DEF;
(2)指出图中所有平行的线段,并说明理由.

第21题图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com