
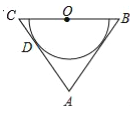
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;(2)根据锐角三角函数,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.
试题解析:(1)证明:如图1,
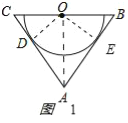
作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=![]() ,AB=12,得OB=8.
,AB=12,得OB=8.
由勾股定理,得AO=4![]() .
.
由三角形的面积,得S△AOB=![]() ABOE=
ABOE=![]() OBAO,
OBAO,
∴OE=![]() =
=![]() ,
,
即半圆O所在圆的半径是![]() .
.


科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其它费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高( )
A.40%
B.33.4%
C.33.3%
D.30%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,有矩形AOBC,点A、B的坐标分别为(0,4)、(10,0),点P的坐标为(2,0),点M在线段AO上,点N在线段AC上,总有∠MPN=90 ,点M从点O运动到点A,当点M运动到A点时,点N与点C重合(如图2)。令AM=x
(1).直接写出点C的坐标___________;
(2)、①设MN2=y,请写出y关于x的函数关系式,并求出y的最小值;
②连接AP交MN于点D,若MN⊥A P,求x的值;
(3)、当点M在边AO上运动时,∠PMN的大小是否发生变化?请说明理由.
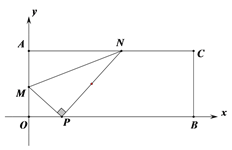
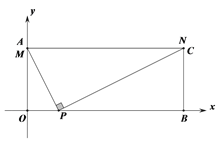
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按如下步骤作图: 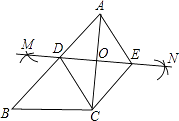
①分别以A、C为圆心,以大于 ![]() AC的长为半径在AC两边作弧,交于两点M、N;
AC的长为半径在AC两边作弧,交于两点M、N;
②连接MN,分别交AB、AC于点D、O;
③过C作CE∥AB交MN于点E,连接AE、CD.
(1)求证:四边形ADCE是菱形;
(2)当∠ACB=90°,BC=6,△ADC的周长为18时,求四边形ADCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,哪些适合抽样调查?哪些适合全面调查?
(1)工厂准备对一批即将出厂的饮料中含有细菌总数的情况进行调查;
(2)小明准备对全班同学所喜爱的球类运动的情况进行调查;
(3)某农田保护区对区内的水稻秧苗的高度进行调查.
查看答案和解析>>
科目:初中数学 来源: 题型:
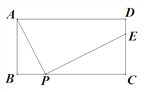
【题目】如图,矩形ABCD中,AB=4,BC=![]() (
(![]() ).P为边BC上一动点(不与B、C重合),过P点作PE⊥AP交直线CD于E.
).P为边BC上一动点(不与B、C重合),过P点作PE⊥AP交直线CD于E.
(1)求证:△ABP∽△PCE;
(2)当P为BC中点时,E恰好为CD的中点,求![]() 的值;
的值;
(3)若![]() =12,DE=1,求BP的长.
=12,DE=1,求BP的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com