
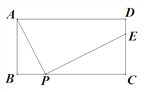
【题目】如图,矩形ABCD中,AB=4,BC=![]() (
(![]() ).P为边BC上一动点(不与B、C重合),过P点作PE⊥AP交直线CD于E.
).P为边BC上一动点(不与B、C重合),过P点作PE⊥AP交直线CD于E.
(1)求证:△ABP∽△PCE;
(2)当P为BC中点时,E恰好为CD的中点,求![]() 的值;
的值;
(3)若![]() =12,DE=1,求BP的长.
=12,DE=1,求BP的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() ,
,![]() ,2,10
,2,10
【解析】试题分析:(1)由四边形ABCD是矩形可得∠B=∠C=90°,由PE⊥AP得∠P=∠PEC,从而可证△ABP∽△PCE;
(2)由△ABP∽△PCE可求出m的值.
(3)由△ABP∽△PCE可求出BP的长.
试题解析:(1)∵四边形ABCD是矩形
∴∠B=∠C=90°
∵PE⊥AP
∴∠APB+∠CPE=90°
∵∠CPE+∠CEP=90°
∴∠APB=∠CEP
∴△ABP∽△PCE
(2)∵P为BC中点时,E为CD的中点,且BC=m,CD=4
∴BP=CP=![]() ,CE=2
,CE=2
∵△ABP∽△PCE
∴![]() 即:
即:![]()
∴m=![]()
即m的值为![]()
(3)设BP的长为x,
∵△ABP∽△PCE,
∴![]()
∴![]() 或
或![]() ,
,
解得x1= ![]() ,x2=
,x2=![]() , x3=2, x4=10
, x3=2, x4=10
∴BP的长为![]() ,
,![]() ,2,10
,2,10


科目:初中数学 来源: 题型:
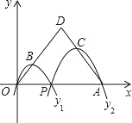
【题目】如图,已知点A(6,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于______________。
查看答案和解析>>
科目:初中数学 来源: 题型:
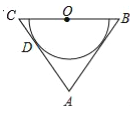
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+1与x轴仅有一个公共点A,经过点A的直线交该抛物线于点B,交y轴于点C,且点C是线段AB的中点.

(1)求这条抛物线对应的函数解析式;
(2)求直线AB对应的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知31=3,32=9,33=27,34=81,35=243,36=729,37=2187,…,请你推测32015的个位数字是( )
A.3
B.9
C.7
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com