
分析 利用射影定理可得AD的长,由勾股定理得CD的长,根据题中条件可知∠B=∠DCA,所以把做题方向转化到△ADC中,用正切即可解答.
解答 解:设AD=x,
∵∠ACB=90°,CD⊥AB,
∴AC2=AD•AB,
即42=x(x+$\frac{9}{5}$),
解得:x=-5(舍去),x=$\frac{16}{5}$,
∴CD=$\frac{12}{5}$,
∵∠B+∠BCD=90°,∠BCD+∠ACD=90°,
∴∠B=∠ACD.
∴tanB=tan∠ACD=$\frac{AD}{CD}$=$\frac{\frac{16}{5}}{\frac{12}{5}}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 此题主要考查了解直角三角形的能力.关键是找出∠B=∠ACD,会利用三角函数的定义求值.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案科目:初中数学 来源: 题型:选择题
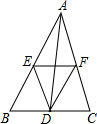 如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )
如图,点D、E、F分别为△ABC各边中点,下列说法正确的是( )| A. | DE=DF | B. | EF=$\frac{1}{2}$AB | C. | S△ABD=S△ACD | D. | AD平分∠BAC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
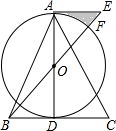 如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.
如图,在△ABC中,AB=AC,AD是BC边上的中线,以AD为直径作⊙O,连接BO并延长至E,使得OE=OB,连接AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:| 看法 | 没有影响 | 影响不大 | 影响很大 |
| 学生人数 | 100 | 60 | m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
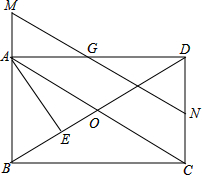 矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )
矩形ABCD中,N、G分别为CD、AD的中点,连接AC、BD交于O,连接NG并延长交BA的延长线于点M,NG交BD于点F,AE⊥BD于点E,则下列结论中:①MG=NG;②S△GDF:S△BOC=1:4;③BC2=2DE•OB;④图中有四对相似三角形,其中正确的结论有( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com