
【题目】如图,在平面直角坐标系中,点C是y轴正半轴上的一个动点,抛物线y=ax2﹣5ax+4a(a是常数,且a>0)过点C,与x轴交于点A、B,点A在点B的左边.连接AC,以AC为边作等边三角形ACD,点D与点O在直线AC两侧.
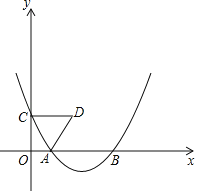
(1)求点A,B的坐标;
(2)当CD∥x轴时,求抛物线的函数表达式;
(3)连接BD,当BD最短时,请直接写出抛物线的函数表达式.
【答案】(1)点A、B的坐标分别为(1,0)、(4,0);(2)y=![]() x2﹣
x2﹣![]() x+
x+![]() ;(3)y=
;(3)y=![]() x2﹣
x2﹣![]() x+
x+![]() .
.
【解析】
(1)根据抛物线解析式求解与x轴的交点坐标即y=0是x的值,即可得出A,B的坐标;
(2)根据三角形ACD是等边三角形可知∠OCA的度数,根据三角函数值可求点C坐标,从而可求答案;
(3)过点D作DE⊥AC于点E,过点D作x轴的垂线于点H,过点E作EF∥x轴交y轴于点F交DH于点G,根据点E坐标进一步求△CFE∽△EGD,进而可求答案.
(1)y=ax2﹣5ax+4a,令y=0,则x=1或4,
∵点A在点B的左边
故点A、B的坐标分别为:(1,0)、(4,0);
(2)∵点A坐标为(1,0),∴OA=1
∵△ACD是等边三角形,∴∠DCA=60°
当CD∥x轴时,∠DCO=90°
∴∠ACO=30°,则∠OCA=60°,
则OC=OAtan60°=![]() ,故点C(0,
,故点C(0,![]() ),
),
即![]() =4a,解得:a=
=4a,解得:a=![]() ,
,
故抛物线的表达式为:![]() ;
;
(3)如图,过点D作DE⊥AC于点E,过点D作x轴的垂线于点H,过点E作EF∥x轴交y轴于点F交DH于点G,
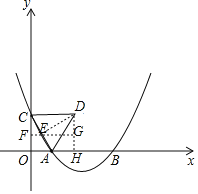
∵△ACD为等边三角形,则点E为AC的中点,则点E(![]() ,2a),AE=CE=
,2a),AE=CE=![]() ED,
ED,
∵∠CEF+∠FCE=90°,∠CEF+∠DEG=90°,∴∠DEG=∠ECF,
∴△CFE∽△EGD,∴![]() ,其中EF=
,其中EF=![]() ,CF=2a,
,CF=2a,
解得:GE=![]() a,DG=
a,DG=![]() ,故点D(
,故点D(![]() ),
),
BD2=(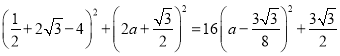 ,
,
故当a=![]() 时,BD最小,
时,BD最小,
故抛物线的表达式为:y=![]() .
.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:初中数学 来源: 题型:
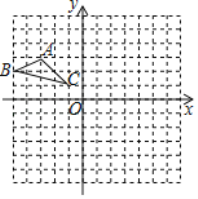
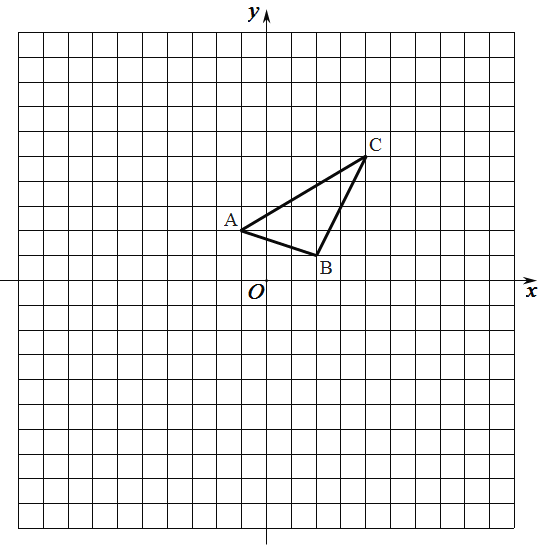
【题目】△ABC在边长为l的正方形网格中如图所示.
①以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2.且△A1B1C位于点C的异侧,并表示出A1的坐标.
②作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
③在②的条件下求出点B经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形网格中建立平面直角坐标系,已知
的正方形网格中建立平面直角坐标系,已知![]() 三个顶点分别为
三个顶点分别为![]() ,
,![]() ,
,![]() .
.
(1)以原点![]() 为位似中心,在
为位似中心,在![]() 轴的上方画出
轴的上方画出![]() ,使
,使![]() 与
与![]() 位似,且相似比为
位似,且相似比为![]() ;
;
(2)![]() 的面积是__________平方单位;
的面积是__________平方单位;
(3)点![]() 为
为![]() 内一点,则在
内一点,则在![]() 内的对应点
内的对应点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E,F分别是锐角∠A两边上的点,AE=AF,分别以点E,F为圆心,以AE的长为半径画弧,两弧相交于点D,连接DE,DF.
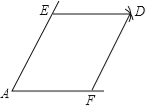
(1)请你判断所画四边形的性状,并说明理由;
(2)连接EF,若AE=8厘米,∠A=60°,求线段EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣3x+2和一次函数y=﹣2x+4,把y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)称为这两个函数的“再生二次函数”,其中t是不为零的实数,其图象记作抛物线L.现有点A(2,0)和抛物线L上的点B(﹣1,n),请完成下列任务:
(尝试)
(1)当t=2时,抛物线y=t(x2﹣3x+2)+(1﹣t)(﹣2x+4)的顶点坐标为 ;
(2)判断点A是否在抛物线L上;
(3)求n的值;
(发现)
通过(2)和(3)的演算可知,对于t取任何不为零的实数,抛物线L总过定点,坐标为 .
(应用)
二次函数y=﹣3x2+5x+2是二次函数y=x2﹣3x+2和一次函数y=﹣2x+4的一个“再生二次函数”吗?如果是,求出t的值;如果不是,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
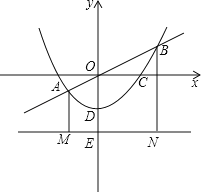
【题目】如图,抛物线![]() (a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
(1)求抛物线的解析式及顶点D的坐标;
(2)点P在抛物线的对称轴上,当△ACP的周长最小时,求出点P的坐标;
(3) 点N在抛物线上,点M在抛物线的对称轴上,是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似,若存在,请求出所有符合条件的点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com