练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在边长为的正方形网格中建立平面直角坐标系，已知三个顶点分别为，，.

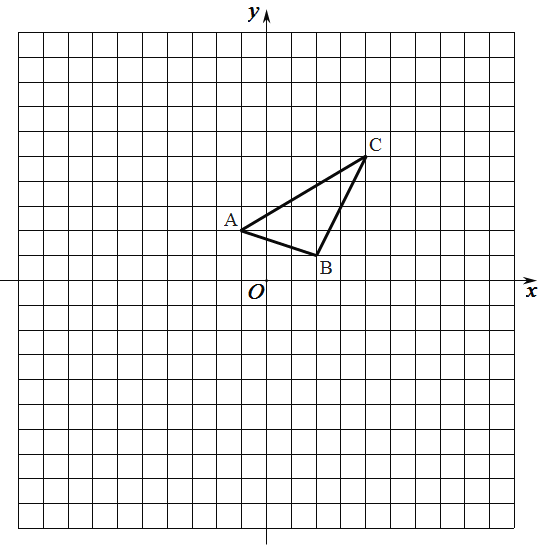
    (1)以原点为位似中心，在轴的上方画出，使与位似，且相似比为；

    (2)的面积是__________平方单位；

    (3)点为内一点，则在内的对应点的坐标为________.

    【答案】(1)见解析；(2)；(3)

    【解析】

    (1)连接OB，延长OB到B1使得OB1=2OB，同法作出A1，C1，连接A1C1， B1C1， A1B1即可．
    (2)两条分割法求出三角形的面积即可．
    (3)利用相似三角形的性质解决问题即可．

    解：(1)△A1B1C1即为所求．
    (2))△A1B1C1的面积=4S△ABC=4(4×512×3×512×1×312×2×4)=28，
    故答案为28．
    (3)点P(a,b)为△ABC内一点，则在△A1B1C1内的对应点P′的坐标为 (2a,2b)，
    故答案为 (2a,2b)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，点D为直线BC上一动点（点D不与B、C重合）以AD为边作正方形ADEF，使∠DAF=∠BAC，连接CF．

    （1）如图1，当点D在线段BC上时，求证：BD=CF；

    （2）如图2，当点D在线段BC的延长线上，且∠BAC=90°时．

    ①问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；

    ②延长BA交CF于点G，连接GE，若AB=2，CD=BC，请求出GE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题：在1～n（n ≥2）这n个自然数中，每次取两个数（不分顺序），使得所取两数之和大于n，共有多少种取法？

    探究：不妨设有m种取法，为了探究m与n的关系，我们先从简单情形入手，再逐次递进，最后猜想得出结论.

    探究一：在1～2这2个自然数中，每次取两个不同的数（不分顺序），使得所取的两个数之和大于2，有多少种取法？

    根据题意，有下列取法：1+2，共1种取法．

    所以，当n=2时，m=1.

    探究二：在1～3这3个自然数中，每次取两个不同的数（不分顺序），使得所取的两个数之和大于3，有多少种取法？

    根据题意，有下列取法：1+3，2+3，共2种取法．

    所以，当n=3时，m=2.

    探究三：在1～4这4个自然数中，每次取两个不同的数（不分顺序），使得所取的两个数之和大于4，有多少种取法？

    根据题意，有下列取法：1+4，2+4，3+4，2+3，共有3+1=4种取法．

    所以，当n=4时，m=3+1=4.

    探究四：在1～5这5个自然数中，每次取两个不同的数（不分顺序），使得所取的两个数之和大于5，有多少种取法？

    根据题意，有下列取法：1+5， 2+5， 3+5， 4+5，2+4，3+4，共有4+2=6种不同的取法．

    所以，当n=5时，m=4+2=6.

    探究五：在1～6这6个自然数中，每次取两个不同的数（不分顺序），使得所取的两个数之和大于6，有多少种不同的取法？（仿照上述探究方法，写出解答过程）

    探究六：在1～7这7个自然数中，每次取两个不同的数，使得所取的两个数之和大于7，共有 种取法？（直接写出结果）

    不妨继续探究n=8,9，···时，m与n的关系.

    结论：在1～n这n个自然数中，每次取两个数，使得所取的两个数字之和大于n，当n为偶数时，共有___种取法；当n为奇数时，共有___种取法；（只填最简算式）

    应用：（1）各边长都是自然数，最大边长为11的不等边三角形共有 个

    （2）各边长都是自然数，最大边长为12的三角形共有 个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知函数（，为常数）的图象经过点.

    （1）求，满足的关系式；

    （2）设该函数图象的顶点坐标是，当的值变化时，求关于的函数解析式；

    （3）若该函数的图象不经过第三象限，当时，函数的最大值与最小值之差为16，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小李的活鱼批发店以 44 元/公斤的价格从港口买进一批 2000 公斤的某品种活鱼，在运输过程中，有部分鱼未能存活，小李对运到的鱼进行随机抽查，结果如表一.由于 市场调节，该品种活鱼的售价与日销售量之间有一定的变化规律，表二是近一段时间该批发店的销售记录.

    表一

    所抽查的鱼的总重量 m(公斤)

    100

    150

    200

    250

    350

    450

    500

    存活的鱼的重量与 m 的比值

    0.885

    0.876

    0.874

    0.878

    0.871

    0.880

    0.880

    表二

    该品种活鱼的售价(元/公斤)

    50

    51

    52

    53

    54

    该品神活鱼的日销售量(公斤)

    400

    360

    320

    280

    240

    (1)请估计运到的 2000 公斤鱼中活鱼的总重量；(直接写出答案)

    (2)按此市场调节的观律，

    ①若该品种活鱼的售价定为 52.5 元/公斤，请估计日销售量，并说明理由；

    ②考虑到该批发店的储存条，小李打算 8 天内卖完这批鱼(只卖活鱼)，且售价保持 不变，求该批发店每日卖鱼可能达到的最大利润，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数y＝ax2+bx+c（a，b，c是常数，且a≠0）的图象如图所示，图象与x轴交点都在点（﹣3，0）的右边，下列结论：①b2＞4ac，②abc＞0，③2a+b﹣c＞0，④a+b+c＜0，其中正确的是（　　）

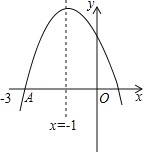
    A.①②B.①②④C.②③D.①②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点C是y轴正半轴上的一个动点，抛物线y＝ax2﹣5ax+4a（a是常数，且a＞0）过点C，与x轴交于点A、B，点A在点B的左边．连接AC，以AC为边作等边三角形ACD，点D与点O在直线AC两侧．

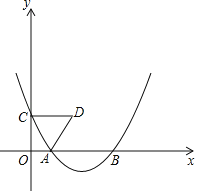
    （1）求点A，B的坐标；

    （2）当CD∥x轴时，求抛物线的函数表达式；

    （3）连接BD，当BD最短时，请直接写出抛物线的函数表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着人们生活质量的提高，净水器已经慢慢走入了普通百姓家庭，某电器公司销售每台进价分别为 2000 元，1700 元的A，B两种型号的净水器，下表是近两周的销售情况：

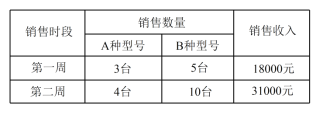
    （1）求A，B两种型号的净水器的销售单价；

    （2）若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台，求 A种型号的净水器最多能采购多少台?

    （3）在（2）的条件下，公司销售完这 30 台净水器能否实现利润超过12800 元的目标?若能，请给出相应的采购方案；若不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图显示了用计算机模拟随机投掷一枚图钉的某次实验的结果．

    下面有三个推断：

    ①当投掷次数是500时，计算机记录“钉尖向上”的次数是308，所以“钉尖向上”的概率是0.616；

    ②随着实验次数的增加，“钉尖向上”的频率总在0.618附近摆动，显示出一定的稳定性，可以估计“钉尖向上”的概率是0.618；

    ③若再次用计算机模拟实验，则当投掷次数为1000时，“钉尖向上”的概率一定是0.620．

    其中合理的是（ ）

    A. ① B. ② C. ①② D. ①③

    查看答案和解析>>

    同步练习册答案