
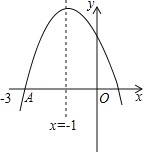
【题目】二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,图象与x轴交点都在点(﹣3,0)的右边,下列结论:①b2>4ac,②abc>0,③2a+b﹣c>0,④a+b+c<0,其中正确的是( )
A.①②B.①②④C.②③D.①②③④
【答案】B
【解析】
根据图像与x轴的交点个数可知二次函数有两个不相等的实数根,所以![]() >0,可判断①;根据图像开口放向,对称轴与y轴的关系和与y轴的交点在正半轴可判断a,b,c的正负,从而可以判断②;根据对称轴为x=-1可判断③;然后即可选出答案.
>0,可判断①;根据图像开口放向,对称轴与y轴的关系和与y轴的交点在正半轴可判断a,b,c的正负,从而可以判断②;根据对称轴为x=-1可判断③;然后即可选出答案.
①由图可知,抛物线与x轴有两个交点,则b2﹣4ac>0,则b2>4ac,故符合题意;
②由图可知,抛物线对称轴在y轴左侧,则a、b同号,即ab>0.又抛物线与y轴交于正半轴,则c>0,所以abc>0,故符合题意;根据对称轴为直线x=﹣1,抛物线与x轴一个交点﹣3<x1<﹣2可判断④.
③由图可知,对称轴x=![]() =﹣1,则b=2a.
=﹣1,则b=2a.
∴2a+b﹣c=4a﹣c,
∵a<0,4a<0,
c>0,﹣c<0,
∴2a+b﹣c=4a﹣c<0,
故不符合题意;
④∵对称轴为直线x=﹣1,抛物线与x轴一个交点﹣3<x1<﹣2,
∴抛物线与x轴另一个交点0<x2<1,
当x=1时,y=a+b+c<0,
故符合题意;
综上所述,正确的结论是:①②④.
故选:B.


科目:初中数学 来源: 题型:
【题目】保护生态环境,建设绿色社会已经从理念变为人们的行动.某化工厂2009年1 月的利润为200万元.设2009年1 月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2009年1 月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
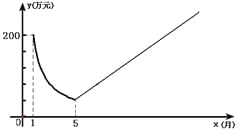
⑴分别求该化工厂治污期间及治污改造工程完工后y与x之间对应的函数关系式.
⑵治污改造工程完工后经过几个月,该厂月利润才能达到2009年1月的水平?
⑶当月利润少于100万元时为该厂资金紧张期,问该厂资金紧张期共有几个月?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:正方形ABCD中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
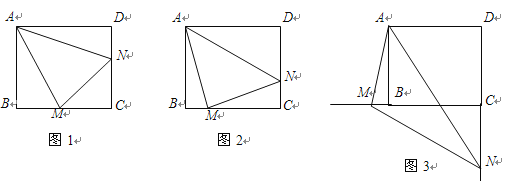
(1)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图1),求证:
时(如图1),求证:![]() ;
;
(2)当![]() 绕点
绕点![]() 旋转到
旋转到![]() 时(如图2),则线段
时(如图2),则线段![]() 和
和![]() 之间数量关系是 ;
之间数量关系是 ;
(3)当![]() 绕点
绕点![]() 旋转到如图3的位置时,猜想线段
旋转到如图3的位置时,猜想线段![]() 和
和![]() 之间又有怎样的的数量关系呢?并对你的猜想加以说明.
之间又有怎样的的数量关系呢?并对你的猜想加以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC 中,AB=AC.
(1)求作△ABC 外接圆(尺规作图)
(2)若△ABC 的外接圆的圆心O到 BC 边的距离为 4,BC=6,求外接圆的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形网格中建立平面直角坐标系,已知
的正方形网格中建立平面直角坐标系,已知![]() 三个顶点分别为
三个顶点分别为![]() ,
,![]() ,
,![]() .
.
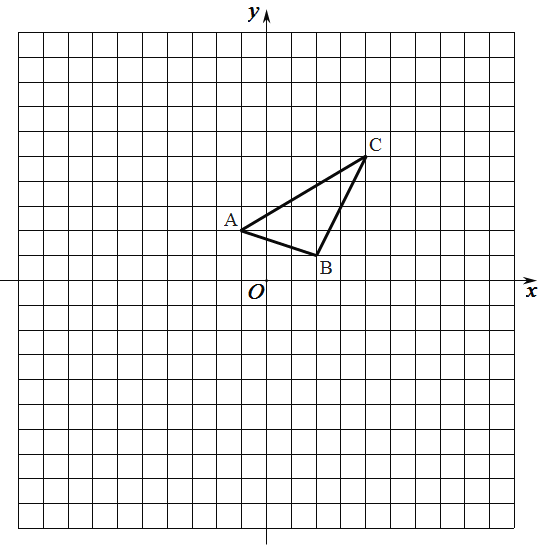
(1)以原点![]() 为位似中心,在
为位似中心,在![]() 轴的上方画出
轴的上方画出![]() ,使
,使![]() 与
与![]() 位似,且相似比为
位似,且相似比为![]() ;
;
(2)![]() 的面积是__________平方单位;
的面积是__________平方单位;
(3)点![]() 为
为![]() 内一点,则在
内一点,则在![]() 内的对应点
内的对应点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
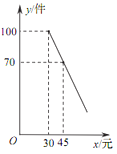
【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料一:一个正整数x能写成x=a2﹣b2(a,b均为正整数,且a≠b),则称x为“雪松数”,a,b为x的一个平方差分解,在x的所有平方差分解中,若a2+b2最大,则称a,b为x的最佳平方差分解,此时F(x)=a2+b2.
例如:24=72﹣52,24为雪松数,7和5为24的一个平方差分解,32=92﹣72,32=62﹣22,因为92+72>62+22,所以9和7为32的最佳平方差分解,F(32)=92+72
材料二:若一个四位正整数,它的千位数字与个位数字相同,百位数字与十位数字相同,但四个数字不全相同,则称这个四位数为“南麓数”.例如4334,5665均为“南麓数”.
根据材料回答:
(1)请直接写出两个雪松数,并分别写出它们的一对平方差分解;
(2)试证明10不是雪松数;
(3)若一个数t既是“雪松数”又是“南麓数”,并且另一个“南麓数”的前两位数字组成的两位数与后两位数字组成的两位数恰好是t的一个平方差分解,请求出所有满足条件的数t中F(t)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
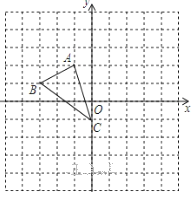
【题目】如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
![]() 作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
作出△ABC 关于原点对称的△A1B1C1,并写出点A1的坐标;
![]() 把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
把△ABC 绕点C逆时针旋转90°,得△A2B2C2,画出△A2B2C2,并写出点A2的坐标;
(3)直接写出△A2B2C2的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com