
【题目】已知:正方形ABCD中,![]() ,
,![]() 绕点
绕点![]() 顺时针旋转,它的两边分别交
顺时针旋转,它的两边分别交![]() (或它们的延长线)于点
(或它们的延长线)于点![]() .
.
(1)当![]() 绕点
绕点![]() 旋转到
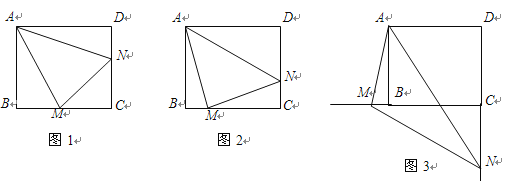
旋转到![]() 时(如图1),求证:
时(如图1),求证:![]() ;
;
(2)当![]() 绕点
绕点![]() 旋转到
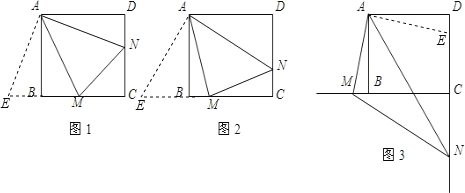
旋转到![]() 时(如图2),则线段
时(如图2),则线段![]() 和
和![]() 之间数量关系是 ;
之间数量关系是 ;
(3)当![]() 绕点
绕点![]() 旋转到如图3的位置时,猜想线段
旋转到如图3的位置时,猜想线段![]() 和
和![]() 之间又有怎样的的数量关系呢?并对你的猜想加以说明.
之间又有怎样的的数量关系呢?并对你的猜想加以说明.
【答案】(1)见解析;
(2)BM+DN=MN;
(3)DNBM=MN,理由见解析.
【解析】
(1)延长CB至E使得BE=DN,连接AE,根据SAS证△ABE≌△ADN,推出∠BAE=∠DAN,AE=AN,求出∠EAM=∠MAN,根据SAS证出△EAM≌△NAM,即可;
(2)证法与(1)类似,延长CB至E,使得BE=DN,连接AE,根据SAS证△ABE≌△ADN,推出∠BAE=∠DAN,AE=AN,求出∠EAM=∠MAN,根据SAS证出△EAM≌△NAM,即可;
(3)DC上截取DE=BM,连接AE,根据SAS证△ADE≌△ABM,推出∠DAE=∠BAM,AE=AM,求出∠EAN=∠MAN.根据SAS证出△MAN≌△EAN即可.
(1)证明:如图1,延长CB至E使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD,![]()
在△ADN和△ABE中
∵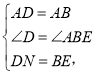
△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴![]()
∵![]()
∴∠EAM=∠MAN,
∵在△EAM和△NAM中
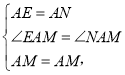
∴△EAM≌△NAM,
∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN;
(2)线段BM,DN和MN之间数量关系是BM+DN=MN,理由如下:
延长CB至E,使得BE=DN,连接AE,
∵四边形ABCD是正方形,
∴AB=AD, ![]()
在△ADN和△ABE中,
∵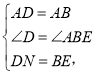
△ABE≌△ADN(SAS),
∴∠BAE=∠DAN,AE=AN,
∴![]()
∵![]()
∴∠EAM=∠MAN,
∵在△EAM和△NAM中
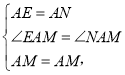
∴△EAM≌△NAM,∴MN=ME,
∵ME=BM+BE=BM+DN,
∴BM+DN=MN,
故答案为BM+DN=MN;
 (3)DNBM=MN,理由如下:
(3)DNBM=MN,理由如下:
如图3,在DC上截取DE=BM,连接AE,
由(1)知△ADE≌△ABM(SAS),
∴∠DAE=∠BAM,AE=AM,
∴![]()
∵![]()
∴∠EAN=∠MAN.
∵在△MAN和△EAN中,
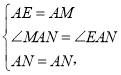
∴△MAN≌△EAN(SAS),
∴EN=MN,
即DNDE=MN,
∴DNBM=MN.


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】某公司投入研发费用40万元(40万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为4元/件.此产品年销售量y(万件)与售价x(元件)之间满足函数关系式y=﹣x+20.
(1)求这种产品第一年的利润W(万元)与售价x(元件)满足的函数关系式;
(2)该产品第一年的利润为24万元,那么该产品第一年的售价是多少?
(3)第二年,该公司将第一年的利润24万元(24万元只计入第二年成本)再次投入研发,使产品的生产成本降为3元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过10万件.请计算该公司第二年的利润W2至少为多少万元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
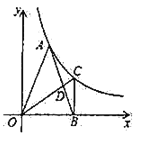
【题目】如图,![]() 为反比例函数
为反比例函数![]() (其中
(其中![]() )图象上的一点,在
)图象上的一点,在![]() 轴正半轴上有一点
轴正半轴上有一点![]() ,
,![]() .连接
.连接![]() ,
,![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)过点![]() 作
作![]() ,交反比例函数
,交反比例函数![]() (其中
(其中![]() )的图象于点
)的图象于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,
,
①求线段![]() 的长;
的长;
②求线段![]() 、
、![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:在1~n(n ≥2)这n个自然数中,每次取两个数(不分顺序),使得所取两数之和大于n,共有多少种取法?
探究:不妨设有m种取法,为了探究m与n的关系,我们先从简单情形入手,再逐次递进,最后猜想得出结论.
探究一:在1~2这2个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于2,有多少种取法?
根据题意,有下列取法:1+2,共1种取法.
所以,当n=2时,m=1.
探究二:在1~3这3个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于3,有多少种取法?
根据题意,有下列取法:1+3,2+3,共2种取法.
所以,当n=3时,m=2.
探究三:在1~4这4个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于4,有多少种取法?
根据题意,有下列取法:1+4,2+4,3+4,2+3,共有3+1=4种取法.
所以,当n=4时,m=3+1=4.
探究四:在1~5这5个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于5,有多少种取法?
根据题意,有下列取法:1+5, 2+5, 3+5, 4+5,2+4,3+4,共有4+2=6种不同的取法.
所以,当n=5时,m=4+2=6.
探究五:在1~6这6个自然数中,每次取两个不同的数(不分顺序),使得所取的两个数之和大于6,有多少种不同的取法?(仿照上述探究方法,写出解答过程)
探究六:在1~7这7个自然数中,每次取两个不同的数,使得所取的两个数之和大于7,共有 种取法?(直接写出结果)
不妨继续探究n=8,9,···时,m与n的关系.
结论:在1~n这n个自然数中,每次取两个数,使得所取的两个数字之和大于n,当n为偶数时,共有___种取法;当n为奇数时,共有___种取法;(只填最简算式)
应用:(1)各边长都是自然数,最大边长为11的不等边三角形共有 个
(2)各边长都是自然数,最大边长为12的三角形共有 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() 为常数)的图象经过点
为常数)的图象经过点![]() .
.
(1)求![]() ,
,![]() 满足的关系式;
满足的关系式;
(2)设该函数图象的顶点坐标是![]() ,当
,当![]() 的值变化时,求
的值变化时,求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)若该函数的图象不经过第三象限,当![]() 时,函数的最大值与最小值之差为16,求
时,函数的最大值与最小值之差为16,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,图象与x轴交点都在点(﹣3,0)的右边,下列结论:①b2>4ac,②abc>0,③2a+b﹣c>0,④a+b+c<0,其中正确的是( )
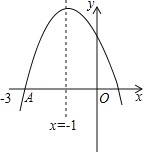
A.①②B.①②④C.②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作DE⊥AC于点E,延长CA交⊙O于点F.

(1)求证:DE是⊙O切线;
(2)若AB=10cm,DE+EA=6cm,求AF的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com