
【题目】如图,矩形ABCD的面积为2016,E、F、G、H分别是边AB,CD的三等分点,则图中阴影四边形的面积为___;若AB·BC=2016,AD:AB=8:9,则阴影四边形的周长为___.
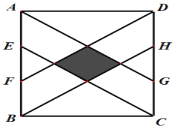
【答案】168; 20![]() .
.
【解析】
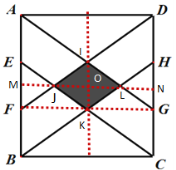
(1)连接KI,连接JL,并延长交AB、CD于点M、N,连接FG,先证四边形IJKL是菱形,然后根据菱形的面积公式求面积;
(2)设AD=8x,AB=9x,根据AB·BC=2016列出方程求出矩形的边长,进一步得到四边形IJKL的对角线长,再利用勾股定理求出菱形的边长和周长.
连接KI,连接JL,并延长交AB、CD于点M、N,连接FG
∵矩形ABCD
∴AB∥CD
∵ E、F、G、H分别是边AB,CD的三等分点
∴AE=![]() AB,CG=
AB,CG=![]() CD,
CD,
∴AE=CG,AE∥CG
∴四边形AECG是平行四边形
∴AG∥CE
同理可证:DF∥BH
∴四边形IJKL是平行四边形
∵AF=DG,AF∥DG,∠FAD=90°
∴四边形AFGD是矩形,
∴IA=ID=IG=IF
∵AI∥EJ
∴![]() 即IJ=
即IJ=![]() FI
FI
同理可证IL=![]() GI
GI
∴JL是△IFG的中位线
∴JL=![]() FG=
FG=![]() BC
BC
∴IJ=IL

∴四边形IJKL是菱形,
∴JL⊥IK,
∵IK=AE=![]() AB
AB
∴S菱形![]() ;
;
∵AB·BC=2016,AD:AB=8:9
设AD=8x,AB=9x
∴72x2=2016
解之:x=2![]()
∴![]()
∴![]()
在Rt△ILO中,![]()
∴菱形IJKL的周长为:![]()
故答案为:168;20![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
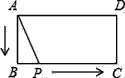
【题目】如图,矩形ABCD中,AB=2,BC=4,P为矩形边上的一个动点,运动路线是A→B→C→D→A,设P点经过的路程为x,以A,P,B为顶点的三角形面积为y,则选项图象能大致反映y与x的函数关系的是( )
A. 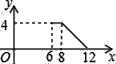 B.
B. 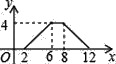 C.
C. 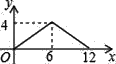 D.
D. 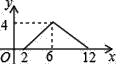
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①为Rt△AOB,∠AOB=90°,其中OA=3,OB=4.将AOB沿x轴依次以A,B,O为旋转中心顺时针旋转.分别得图②,图③,…,则旋转到图⑩时直角顶点的坐标是_____.
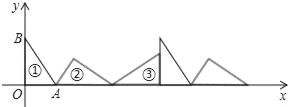
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列因式分解的过程,再回答所提出的问题:
1+x+x(x+1)+x(x+1)2=(1+x)[1+x+x(x+1)]
=(1+x)2(1+x)
=(1+x)3
(1)上述分解因式的方法是 ,共应用了 次.
(2)若分解1+x+x(x+1)+x(x+1)2+…+ x(x+1)2004,则需应用上述方法 次,结果是 .
(3)分解因式:1+x+x(x+1)+x(x+1)2+…+ x(x+1)n(n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+2019x+m=0与x2+mx+2019=0有且只有一个公共根,m的值为( )
A. 2019B. -2019C. 2020D. -2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )

A. (2,12)
B. (﹣2,0)
C. (2,12)或(﹣2,0)
D. (12,2)或(﹣2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象与反比例函数y=![]() 的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
的图象相交于点A(m,3)、B(﹣6,n),与x轴交于点C.
(1)求一次函数y=kx+b的关系式;
(2)结合图象,直接写出满足kx+b>![]()
![]() 的x的取值范围;
的x的取值范围;
(3)若点P在x轴上,且S△ACP=![]() S△BOC,求点P的坐标.
S△BOC,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com