
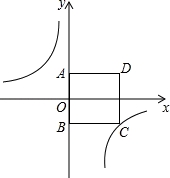
如图,在正方形ABCD中,点A在y轴正半轴上,点B的坐标为(0,﹣3),反比例函数y=﹣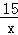 的图象经过点C.
的图象经过点C.
(1)求点C的坐标;
(2)若点P是反比例函数图象上的一点且S△PAD=S正方形ABCD;求点P的坐标.
【考点】反比例函数图象上点的坐标特征;反比例函数系数k的几何意义.
【分析】(1)先由点B的坐标为(0,﹣3)得到C的纵坐标为﹣3,然后代入反比例函数的解析式求得横坐标为5,即可求得点C的坐标为(5,﹣3);
(2)设点P到AD的距离为h,利用△PAD的面积恰好等于正方形ABCD的面积得到h=10,再分类讨论:当点P在第二象限时,则P点的纵坐标yP=h+2=12,可求的P点的横坐标,得到点P的坐标为(﹣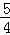 ,12);②当点P在第四象限时,P点的纵坐标为yP=﹣(h﹣2)=﹣8,再计算出P点的横坐标.于是得到点P的坐标为(
,12);②当点P在第四象限时,P点的纵坐标为yP=﹣(h﹣2)=﹣8,再计算出P点的横坐标.于是得到点P的坐标为(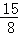 ,﹣8).
,﹣8).
【解答】解:(1)∵点B的坐标为(0,﹣3),
∴点C的纵坐标为﹣3,
把y=﹣3代入y=﹣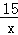 得,﹣3=﹣
得,﹣3=﹣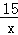
解得x=5,
∴点C的坐标为(5,﹣3);
(2)∵C(5,﹣3),
∴BC=5,
∵四边形ABCD是正方形,
∴AD=5,
设点P到AD的距离为h.
∵S△PAD=S正方形ABCD,
∴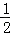 ×5×h=52,
×5×h=52,
解得h=10,
①当点P在第二象限时,yP=h+2=12,
此时,xP=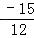 =﹣
=﹣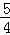 ,
,
∴点P的坐标为(﹣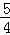 ,12),
,12),
②当点P在第四象限时,yP=﹣(h﹣2)=﹣8,
此时,xP=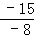 =
=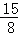 ,
,
∴点P的坐标为(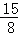 ,﹣8).
,﹣8).
综上所述,点P的坐标为(﹣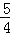 ,12)或(
,12)或(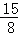 ,﹣8).
,﹣8).
【点评】本题考查了反比例函数图象上点的坐标特征,求得C点的坐标是解题的关键.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
某市在旧城改造中,计划在市内一块如图所示的三角形空地上种植草皮以美化环境,已知这种草皮每平方米售价a元,则购买这种草皮至少需要( ).
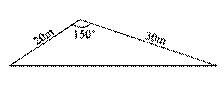
10题图
(A)450a元 (B)225a元
(C)150a元 (D)300a元
查看答案和解析>>
科目:初中数学 来源: 题型:
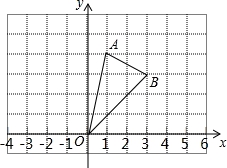
如图,△AOB的三个顶点都在网格的格点上,每个小正方形的边长均为1个单位长度.
(1)在网格中画出△AOB绕点O逆时针旋转90°后的△A1OB1的图形;
(2)求旋转过程中边OB扫过的面积(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,D,E分别是AB,AC边上的中点,连接DE,那么△ADE与△ABC的面积之比是( )
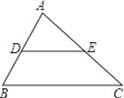

A.1:16 B.1:9 C.1:4 D.1:2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com