练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，在△ABC中，D，E分别是AB，AC边上的中点，连接DE，那么△ADE与△ABC的面积之比是（　　）

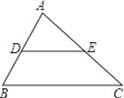
    A．1：16       B．1：9  C．1：4 D．1：2

    　


    C【考点】相似三角形的判定与性质；三角形中位线定理．

    【专题】计算题．

    【分析】由于D，E分别是AB，AC边上的中点，利用三角形中位线定理可知DE∥BC，=，再利用平行线分线段成比例定理的推论易证△ADE∽△ABC，再利用相似三角形面积比等于相似比的平方可求两个三角形面积比．

    【解答】解：∵D，E分别是AB，AC边上的中点，

    ∴DE∥BC，=，

    ∴△ADE∽△ABC，

    ∴S△ADE：S△ABC=（）2=．

    故选C．

    【点评】本题考查了相似三角形的判定和性质、平行线分线段成比例定理的推论、三角形中位线定理．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    △ABC中，AB＝AC＝4，点P在BC边上运动，猜想AP2＋PB·PC的值是否随点P位置的变化而变化，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


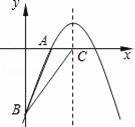
    如图，已知二次函数y=﹣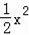+bx+c的图象经过A（2，0）、B（0，﹣6）两点．

    （1）求这个二次函数的解析式；

    （2）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    x2﹣2x﹣3=0             

    查看答案和解析>>

    科目：初中数学 来源： 题型：


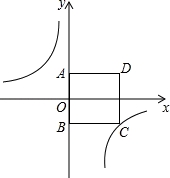
    如图，在正方形ABCD中，点A在y轴正半轴上，点B的坐标为（0，﹣3），反比例函数y=﹣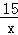的图象经过点C．

    （1）求点C的坐标；

    （2）若点P是反比例函数图象上的一点且S△PAD=S正方形ABCD；求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，某个反比例函数的图象经过点P，则它的解析式为（　　）

    A．y=（x＞0）   B．y=（x＞0）     C．y=（x＜0）   D．y=（x＜0）

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某网店一种玩具原价为100元，“双十一”期间，经过两次降价，售价变成了81元，假设两次降价的百分率相同，则每次降价的百分率为　　　　　　．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出的方程是（　　）

    A．（3+x）（4﹣0.5x）=15  B．（x+3）（4+0.5x）=15   C．（x+4）（3﹣0.5x）=15  D．（x+1）（4﹣0.5x）=15

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若=1，则   （    ）

    A. x≠0          B. x≠2         C. x≠            D. x为任意有理数

    查看答案和解析>>

    同步练习册答案