
某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15 C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
如图,在△ABC中,D,E分别是AB,AC边上的中点,连接DE,那么△ADE与△ABC的面积之比是( )
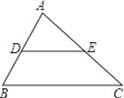

A.1:16 B.1:9 C.1:4 D.1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB表示路灯,当身高为1.6米的小名站在离路灯1.6的D处时,他测得自己在路灯下的影长DE与身高CD相等,当小明继续沿直线BD往前走到E点时,画出此时小明的影子,并计算此时小明的影长.
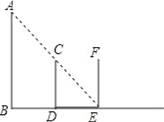

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是x=2,与x轴的一个交点是(﹣1,0),有下列结论:
①abc>0;
②4a﹣2b+c<0;
③4a+b=0;
④抛物线与x轴的另一个交点是(5,0);
⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1=y2.
其中正确的是( )
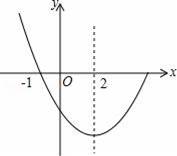

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
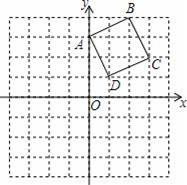
每个小方格都是边长为1个单位长度,正方形ABCD在坐标系中的位置如图所示.
(1)画出正方形ABCD关于原点中心对称的图形;
(2)画出正方形ABCD绕点D点顺时针方向旋转90°后的图形;
(3)求出正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线.

查看答案和解析>>
科目:初中数学 来源: 题型:
把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积。
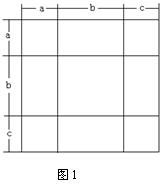
⑴如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为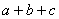 的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来。
的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来。
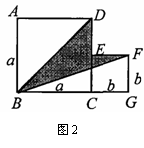
⑵如图2,是将两个边长分别为 和
和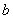 的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足
的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足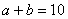 ,
,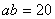 ,你能求出阴影部分的面积吗?
,你能求出阴影部分的面积吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com