练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    把抛物线y=x2+bx+c向左平移2个单位，再向上平移3个单位，得到抛物线y=x2﹣2x+1，则原来的抛物线　　　　　　．


    　y=x2﹣6x+1　．

    【考点】二次函数图象与几何变换．

    【分析】此题实际上是求把抛物线y=x2﹣2x+1向右平移2个单位，再向下平移3个单位后得到抛物线的解析式．根据“上加下减，左加右减”的规律解答即可．

    【解答】解：∵y=x2﹣2x+1=（x﹣1）2，

    ∴将抛物线y=x2﹣2x+1向右平移2个单位，再向下平移3个单位后得到抛物线的解析式为：y=（x﹣1﹣2）2﹣3=x2﹣6x+1，即y=x2﹣6x+1．

    故答案是：y=x2﹣6x+1．

    【点评】本题主要考查了抛物线的顶点坐标的求法及抛物线平移不改变二次项的系数的值，难度适中．

    　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若一个直角三角形的两边长分别为12和5，则此三角形的第三边长为______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，AB＝AC＝4，点P在BC边上运动，猜想AP2＋PB·PC的值是否随点P位置的变化而变化，并证明你的猜想．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：，其中，.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列图形中，是中心对称图形的是（　　）

    A． B． C．  D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    观察下列图形规律：当n=　　　　　　时，图形“●”的个数和“△”的个数相等．

    　

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


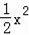
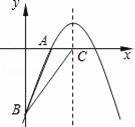
    如图，已知二次函数y=﹣+bx+c的图象经过A（2，0）、B（0，﹣6）两点．

    （1）求这个二次函数的解析式；

    （2）设该二次函数的对称轴与x轴交于点C，连接BA、BC，求△ABC的面积．

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    x2﹣2x﹣3=0             

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某种花卉每盆的盈利与每盆的株数有一定的关系，每盆植3株时，平均每株盈利4元；若每盆增加1株，平均每株盈利减少0.5元，要使每盆的盈利达到15元，每盆应多植多少株？设每盆多植x株，则可以列出的方程是（　　）

    A．（3+x）（4﹣0.5x）=15  B．（x+3）（4+0.5x）=15   C．（x+4）（3﹣0.5x）=15  D．（x+1）（4﹣0.5x）=15

    　

    查看答案和解析>>

    同步练习册答案