
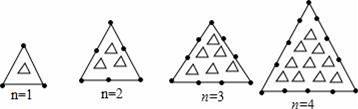
观察下列图形规律:当n= 时,图形“●”的个数和“△”的个数相等.

5
【考点】规律型:图形的变化类.
【专题】规律型.
【分析】首先根据n=1、2、3、4时,“●”的个数分别是3、6、9、12,判断出第n个图形中“●”的个数是3n;然后根据n=1、2、3、4,“△”的个数分别是1、3、6、10,判断出第n个“△”的个数是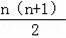
 ;最后根据图形“●”的个数和“△”的个数相等,求出n的值是多少即可.
;最后根据图形“●”的个数和“△”的个数相等,求出n的值是多少即可.
【解答】解:∵n=1时,“●”的个数是3=3×1;
n=2时,“●”的个数是6=3×2;
n=3时,“●”的个数是9=3×3;
n=4时,“●”的个数是12=3×4;
∴第n个图形中“●”的个数是3n;
又∵n=1时,“△”的个数是1=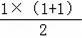
 ;
;
n=2时,“△”的个数是3=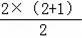
 ;
;
n=3时,“△”的个数是6=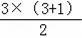
 ;
;
n=4时,“△”的个数是10=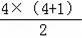
 ;
;
∴第n个“△”的个数是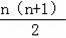
 ;
;
由3n=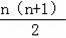
 ,
,
可得n2﹣5n=0,
解得n=5或n=0(舍去),
∴当n=5时,图形“●”的个数和“△”的个数相等.
故答案为:5.
【点评】此题主要考查了规律型:图形的变化类问题,要熟练掌握,解答此类问题的关键是:首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.


科目:初中数学 来源: 题型:
下列事件中,必然事件是( )
A.打开电视,它正在播广告
B.掷两枚质地均匀的正方体骰子,点数之和一定大于6
C.早晨的太阳从东方升起
D.没有水分,种子发芽
查看答案和解析>>
科目:初中数学 来源: 题型:
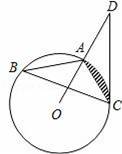
如图,已知△ABC是⊙O的内接三角形,D是OA延长线上的一点,连接DC,且∠B=∠D=30°,AC=4.
(1)判断直线CD与⊙O的位置关系,并说明理由;
(2)求阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
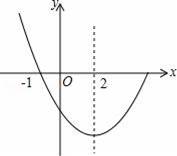
如图,是抛物线y=ax2+bx+c(a≠0)图象的一部分,已知抛物线的对称轴是x=2,与x轴的一个交点是(﹣1,0),有下列结论:
①abc>0;
②4a﹣2b+c<0;
③4a+b=0;
④抛物线与x轴的另一个交点是(5,0);
⑤点(﹣3,y1),(6,y2)都在抛物线上,则有y1=y2.
其中正确的是( )

A.4个 B.3个 C.2个 D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com