
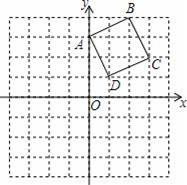
每个小方格都是边长为1个单位长度,正方形ABCD在坐标系中的位置如图所示.
(1)画出正方形ABCD关于原点中心对称的图形;
(2)画出正方形ABCD绕点D点顺时针方向旋转90°后的图形;
(3)求出正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线.

【考点】作图-旋转变换.
【专题】作图题.
【分析】(1)根据关于原点中心对称的点的坐标特征写出A、B、C、D的对应点A′、B′、C′、D′的坐标,然后描点即可得到正方形A′B′C′D′;
(2)根据网格特点、正方形的性质和旋转的性质画出点C和B的对应点E和F,则可得到正方形ABCD绕点D点顺时针方向旋转90°后的正方形CFED;
(3)由于点B绕点D点顺时针方向旋转90°后经过的路径为以D点为圆心,半径为BD,圆心角为90度的弧,于是根据弧长公式可求解.
【解答】解:(1)如图,正方形A′B′C′D′为所作;
(2)如图,正方形CFED为所作;
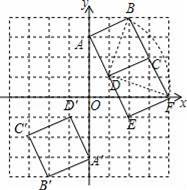

(3)BD=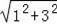
 =
=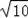
 ,
,
所以正方形ABCD的点B绕点D点顺时针方向旋转90°后经过的路线长=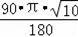
 =
=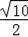
 π.
π.
【点评】本题考查了作图﹣旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


科目:初中数学 来源: 题型:
如图,已知二次函数y=﹣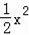
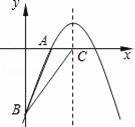
 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
某种花卉每盆的盈利与每盆的株数有一定的关系,每盆植3株时,平均每株盈利4元;若每盆增加1株,平均每株盈利减少0.5元,要使每盆的盈利达到15元,每盆应多植多少株?设每盆多植x株,则可以列出的方程是( )
A.(3+x)(4﹣0.5x)=15 B.(x+3)(4+0.5x)=15 C.(x+4)(3﹣0.5x)=15 D.(x+1)(4﹣0.5x)=15
查看答案和解析>>
科目:初中数学 来源: 题型:
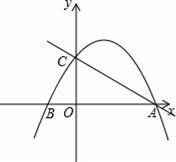
在平面直角坐标系中,已知点B的坐标是(﹣1,0),点A的坐标是(4,0),点C的坐标是(0,4),抛物线过A、B、C三点.
(1)求抛物线的解析式.
(2)点N事抛物线上的一点(点N在直线AC上方),过点N作NG⊥x轴,垂足为G,交AC于点H,当线段ON与CH互相平分时,求出点N的坐标.
(3)设抛物线的对称轴为直线L,顶点为K,点C关于L的对称点J,x轴上是否存在一点Q,y轴上是否一点R使四边形KJQR的周长最小?若存在,请求出周长的最小值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是( )
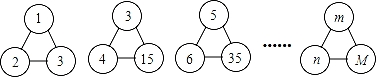
A.M=mn B.M=n(m+1) C.M=mn+1 D.M=m(n+1)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com