
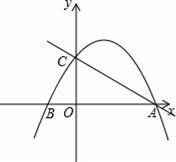
��ƽ��ֱ������ϵ�У���֪��B�������ǣ���1��0������A�������ǣ�4��0������C�������ǣ�0��4���������߹�A��B��C���㣮
��1���������ߵĽ���ʽ��
��2����N���������ϵ�һ�㣨��N��ֱ��AC�Ϸ���������N��NG��x�ᣬ����ΪG����AC�ڵ�H�����߶�ON��CH����ƽ��ʱ�������N�����꣮
��3���������ߵĶԳ���Ϊֱ��L������ΪK����C����L�ĶԳƵ�J��x�����Ƿ����һ��Q��y�����Ƿ�һ��Rʹ�ı���KJQR���ܳ���С�������ڣ�������ܳ�����Сֵ���������ڣ���˵�����ɣ�

��
�����㡿���κ����ۺ��⣮
����������1�����ݴ���ϵ�������ɵú�������ʽ��
��2�����ݶԽ�����ƽ�ֵ��ı�����ƽ���ı��Σ��ɵ�NH��OC�Ĺ�ϵ�����ݽⷽ�̣��ɵ�m��ֵ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
��3�������߶δ�ֱƽ�����ϵĵ㵽�߶����˵�ľ�����ȣ��ɵ�DR��DK�ij���QJ��QE�Ĺ�ϵ����������֮���߶���̣��ɵ�KR+RQ+QJ=ED�����ݹ��ɶ������ɵ�DE�ij���KJ�ij���
����𡿽⣺��1���������ߵĽ���ʽΪy=ax2+bx+c����A��B��C��������뺯������ʽ����
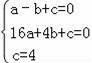
 ��
��
���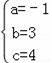
 ��
��
�����ߵĽ���ʽΪy=��x2+3x+4��
��2����ͼ1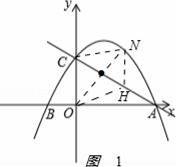
 ��
��
��AC�Ľ���ʽΪy=kx+b����A��C��������룬��
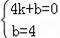
 �����
�����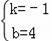
 ��
��
AC�Ľ���ʽΪy=��x+4��
��N��m����m2+3m+4����H��m����m+4����
NH=��m2+4m��
���߶�ON��CH����ƽ�֣���
NH=OC=4��
����m2+4m=4��
���m=2����m2+3m+4=6����N��2��6����
���߶�ON��CH����ƽ��ʱ����N������Ϊ��2��6����
��3����ͼ2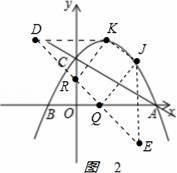
 ��
��
��K�����y��ĶԳƵ�D����J�����x��ĶԳƵ�E������DE��y����R��x����Q�㣬
y=��x2+3x+4=����x��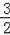
 ��2+
��2+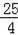
 ������K��
������K��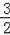
 ��
��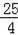
 ����
����
�ɵ�C���ڶԳ���L=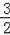
 �ĶԳƵ�J��C��0��4������
�ĶԳƵ�J��C��0��4������
J��������3��4����
��K�����y��ĶԳƵ�D��K��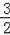
 ��
��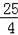
 ������
������
D����������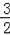
 ��
��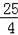
 ����
����
��J�����x��ĶԳƵ�E��J��3��4������
E���������3����4����
�ɹ��ɶ�������KJ=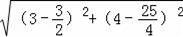
 =
=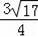
 ��
��
DE=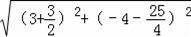
 =
=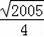
 ��
��
KJQR���ܳ���С=KR+RQ+QJ+KJ=DE+KJ=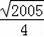
 +
+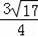
 ��
��
�����������⿼���˶��κ����ۺ��⣬���ô���ϵ������������ʽ������ƽ���ı��ε��ж������ʵó�����m�ķ����ǽ���ؼ��������߶δ�ֱƽ���ߵ����ʵó�DR��DK�ij���QJ��QE�Ĺ�ϵ�ǽ���ؼ���
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪����x��һԪ���η��̣�a﹣1��x2+x+a2﹣1=0��һ������0����a��ֵΪ( )
A��1 B��﹣1 C��1��﹣1 D��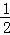
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��AB��ʾ·�ƣ�������Ϊ1.6��С��վ����·��1.6��D��ʱ��������Լ���·���µ�Ӱ��DE������CD��ȣ���С��������ֱ��BD��ǰ�ߵ�E��ʱ��������ʱС����Ӱ�ӣ��������ʱС����Ӱ����
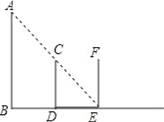

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ����������y=ax2+bx+c��a��0��ͼ���һ���֣���֪�����ߵĶԳ�����x=2����x���һ�������ǣ���1��0���������н��ۣ�
��abc��0��
��4a��2b+c��0��
��4a+b=0��
����������x�����һ�������ǣ�5��0����
�ݵ㣨��3��y1������6��y2�������������ϣ�����y1=y2��
������ȷ���ǣ�������
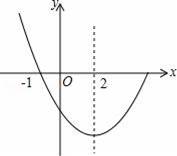

A��4�� B��3�� C��2�� D��1��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
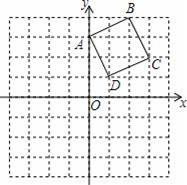
ÿ��С�����DZ߳�Ϊ1����λ���ȣ�������ABCD������ϵ�е�λ����ͼ��ʾ��
��1������������ABCD����ԭ�����ĶԳƵ�ͼ�Σ�
��2������������ABCD�Ƶ�D��˳ʱ�뷽����ת90����ͼ�Σ�
��3�����������ABCD�ĵ�B�Ƶ�D��˳ʱ�뷽����ת90�����·�ߣ�

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
���������У�����������ǣ�������
A�����������ζ����� B���ȱ������ζ�����
C����������ζ����� D��ֱ�������ζ�����
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
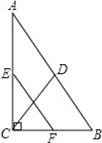
��ͼ����Rt��ABC�У���ACB=90�㣬��D��E��F�ֱ�ΪAB��AC��BC���е㣮��CD=5����EF�ij�Ϊ��������������

��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
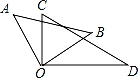
��ͼ���������ǰ��ֱ�Ƕ����ص���һ�𣬡�DOB���DOA�ı���2��11�����BOC=��������������
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com