
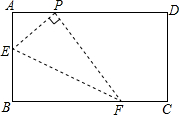
 如图,在矩形ABCD中,点P在AD上,AB=2,AP=1,E是AB上的一个动点,连接PE,过点P作PE的垂线,交BC于点F,连接EF,设EF的中点为G,当点E从点B运动到点A时,点G移动的路径的长是$\sqrt{5}$.
如图,在矩形ABCD中,点P在AD上,AB=2,AP=1,E是AB上的一个动点,连接PE,过点P作PE的垂线,交BC于点F,连接EF,设EF的中点为G,当点E从点B运动到点A时,点G移动的路径的长是$\sqrt{5}$. 分析 设点E的坐标为(0,m),先求得EP的解析式,从而可得到PF的解析式(含字母m的式子),从而可解得点F的坐标,由线段中点坐标公式可求得点G的坐标,从而可得到点G的轨迹是一条线段,然后求得线段端点的坐标,最后利用两点间的距离公式求解即可.
解答 解:设点E的坐标为(0,m),直线EP的解析式为y=kx+m.
将x=1,y=2,得:k+m=2,
解得:k=2-m.
∵PE⊥PF,
∴直线EP与直线PF的一次项系数的乘积为-1.
设直线PF的解析式为:y1-2=$\frac{1}{m-2}$(x-1).
将y1=0代入得:.x=5-2m.
∴点F的坐标为(5-2m,0).
由中点坐标公式可知点G的坐标为($\frac{5-2m}{2}$,$\frac{m}{2}$),即x=$\frac{5-2m}{2}$,y=$\frac{m}{2}$.
∴y=$-\frac{1}{2}x+\frac{5}{4}$.
∴点G的轨迹是一条线段.
当m=0时,点G的坐标为($\frac{5}{2}$,0);当m=2时,点G的坐标为($\frac{1}{2}$,1).
由两点之间的距离公式得;点G移动的路径的长=$\sqrt{(\frac{5}{2}-\frac{1}{2})^{2}+(1-0)^{2}}$=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题主要考查的是点的轨迹问题,求得点G运动路线的解析式,判断出点G运动的轨迹是一条线段是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
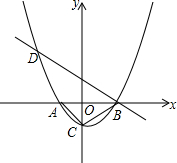 如图,已知抛物线y=m(x+1)(x-2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
如图,已知抛物线y=m(x+1)(x-2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
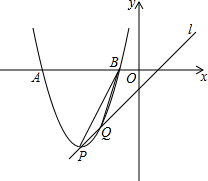 已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.
已知抛物线y=x2-2mx+m2+m-1(m是常数)的顶点为P,直线l:y=x-1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com