练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    函数y=中自变量x的取值范围是　


    x≤1　．

    【考点】函数自变量的取值范围．

    【分析】根据被开方数大于等于0列式计算即可得解．

    【解答】解：由题意得，1﹣x≥0，

    解得x≤1．

    故答案为：x≤1．

    【点评】本题考查了函数自变量的范围，一般从三个方面考虑：

    （1）当函数表达式是整式时，自变量可取全体实数；

    （2）当函数表达式是分式时，考虑分式的分母不能为0；

    （3）当函数表达式是二次根式时，被开方数非负．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，下列能判定AB∥CD的条件有（　　）个．

    （1）∠B+∠BCD=180°；（2）∠1=∠2；（3）∠3=∠4；（4）∠B=∠5．

    A．1       B．2       C．3       D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，点A、B、C在半径为9的⊙O上，的长为2π，则∠ACB的大小是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初中学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：

    （1）在这次评价中，一共抽查了　560　名学生；

    （2）在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为　54　度；

    （3）请将频数分布直方图补充完整；

    （4）如果全市有6000名初三学生，那么在试卷评讲课中，“独立思考”的初三学生约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系中，A（1，4），B（3，2），点C是直线y=﹣4x+20上一动点，若OC恰好平分四边形OACB的面积，则C点坐标为　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    菱形具有而矩形不一定具有的性质是（　　）

    A．对角线互相垂直     B．对角线相等

    C．对角线互相平分     D．对角互补

    查看答案和解析>>

    科目：初中数学 来源： 题型：


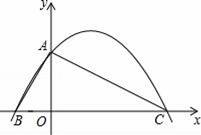
    已知，如图，在平面直角坐标系中，△ABC的边BC在x轴上，顶点A在y轴的正半轴上，OA=2，OB=1，OC=4．

    （1）求过A、B、C三点的抛物线的解析式；

    （2）设点G是对称轴上一点，求当△GAB周长最小时，点G的坐标；

    （3）若抛物线对称轴交x轴于点P，在平面直角坐标系中，是否存在点Q，使△PAQ是以PA为腰的等腰直角三角形？若存在，写出所有符合条件的点Q的坐标，并选择其中一个的加以说明；若不存在，说明理由；

    （4）设点M是x轴上的动点，试问：在平面直角坐标系中，是否存在点N，使得以点A、B、M、N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，将斜边长为4的直角三角板放在直角坐标系xOy中，两条直角边分别与坐标轴重合，P为斜边的中点．现将此三角板绕点O顺时针旋转120°后点P的对应点的坐标是（　　）

    A．（，1）     B．（1，﹣）  C．（2，﹣2）       D．（2，﹣2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，四边形ABCD是菱形，对角线AC与BD交于点O，且AC=80，BD=60．动点M、N分别以每秒1个单位的速度从点A、D同时出发，分别沿A→O→D和D→A运动，当点N到达点A时，M、N同时停止运动．设运动时间为t秒．

    （1）求菱形ABCD的周长；

    （2）记△DMN的面积为S，求S关于t的解析式，并求S的最大值；

    （3）当t=30秒时，在线段OD的垂直平分线上是否存在点P，使得∠DPO=∠DON？若存在，这样的点P有几个？并求出点P到线段OD的距离；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案