练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，点A、B、C在半径为9的⊙O上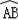，的长为2π，则∠ACB的大小是　　．


    20°【考点】弧长的计算；圆周角定理．

    【分析】连结OA、OB．先由的长为2π，利用弧长计算公式求出∠AOB=40°，再根据在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半得到∠ACB=∠AOB=20°．

    【解答】解：连结OA、OB．设∠AOB=n°．

    ∵的长为2π，

    ∴=2π，

    ∴n=40，

    ∴∠AOB=40°，

    ∴∠ACB=∠AOB=20°．

    故答案为20°．

    【点评】本题考查了弧长公式：l=（弧长为l，圆心角度数为n，圆的半径为R），同时考查了圆周角定理．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    南京地铁三号线全长为44830米，将44830用科学记数法表示为　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


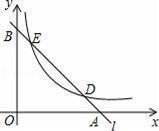
    已知直线l分别与x轴、y轴交于A、B两点，与双曲线y=（m≠0，x＞0）分别交于D、E两点，若点D的坐标为（4，1），点E的坐标为（1，n）

    （1）分别求出直线l与双曲线的解析式；

    （2）求△EOD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    今年3月5日，李克强总理在《政府工作报告》中指出，到2020年，我国经济总量将超过90万亿元，90万亿元用科学记数法表示为（　　）

    A．9×1011元  B．90×1010元       C．9×1012元  D．9×1013元

    查看答案和解析>>

    科目：初中数学 来源： 题型：


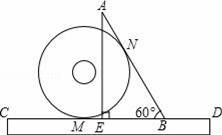
    小明把半径为1的光盘、直尺和三角尺形状的纸片按如图所示放置于桌面上，此时，光盘与AB，CD分别相切于点N，M．现从如图所示的位置开始，将光盘在直尺边上沿着CD向右滚动到再次与AB相切时，光盘的圆心经过的距离是　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    等腰三角形边长分别为a，b，2，且a，b是关于x的一元二次方程x2﹣6x+n﹣1=0的两根，则n的值为

    （　　）

    A．9       B．10     C．9或10     D．8或10

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知抛物线y=x2+bx+c与x轴交与A、B两点（A点在B点左侧），与y轴交与点C（0，﹣3），对称轴是直线x=1，直线BC与抛物线的对称轴交与点D．

    （1）求抛物线的函数关系式．

    （2）若平行于x轴的直线与抛物线交于点M、N（M点在N点左侧），且MN为直径的圆与x轴相切，求该圆的半径．

    （3）若点M在第三象限，记MN与y轴的交点为点F，点C关于点F的对称点为点E．

    ①当线段MN=AB时，求tan∠CED的值；

    ②当以C、D、E为顶点的三角形是直角三角形时，请直接写出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    函数y=中自变量x的取值范围是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，DB⊥DC，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M．点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．

    （1）求经过B、E、C三点的抛物线的解析式；

    （2）是否存在点P，使得以P、Q、M为顶点的三角形与△AOD相似？若存在，求出满足条件的点P的坐标；若不存在，请说明理由；

    （3）若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由．

    查看答案和解析>>

    同步练习册答案