
已知抛物线y=x2+bx+c与x轴交与A、B两点(A点在B点左侧),与y轴交与点C(0,﹣3),对称轴是直线x=1,直线BC与抛物线的对称轴交与点D.
(1)求抛物线的函数关系式.
(2)若平行于x轴的直线与抛物线交于点M、N(M点在N点左侧),且MN为直径的圆与x轴相切,求该圆的半径.
(3)若点M在第三象限,记MN与y轴的交点为点F,点C关于点F的对称点为点E.
①当线段MN=
 AB时,求tan∠CED的值;
AB时,求tan∠CED的值;
②当以C、D、E为顶点的三角形是直角三角形时,请直接写出点M的坐标.


【考点】二次函数综合题.
【专题】代数几何综合题.
【分析】(1)把点C的坐标代入函数解析式求出c,再根据对称轴求出b,即可得解;
(2)设圆的半径为r,则MN=2r,再分直线MN在x轴上方与下方两种情况表示出点N的坐标,然后代入抛物线解析式计算即可求出r;
(3)①令y=0解关于x的一元二次方程求出点A、B的坐标,从而得到AB,再求出MN的长度,根据抛物线的对称性求出点N的横坐标,再代入抛物线解析式求出点N的纵坐标,即点F的纵坐标,再根据点的对称求出点E的坐标,设直线BC的解析式为y=kx+b(k≠0,k、b为常数),利用待定系数法求出直线BC的解析式,再求出点D的坐标,然后根据点D、E的坐标,利用锐角的正切的定义列式计算即可得解;
②根据直线BC的解析式可得∠BCO=45°,然后分∠CDE=90°时,△CDE是等腰直角三角形,根据等腰直角三角形的性质,点F与点D的纵坐标相同,即为点M的纵坐标,然后代入抛物线解析式,计算即可得到点M的坐标;∠CED=90°时,点E与点D的纵坐标相同,根据对称性求出点F的纵坐标,即为点M的纵坐标,然后代入抛物线解析式,计算即可得到点M的坐标.
【解答】解:(1)∵抛物线y=x2+bx+c与y轴交于点C(0,﹣3),
∴c=﹣3,
对称轴为直线x=﹣
 =1,
=1,
∴b=﹣2,
∴抛物线的函数关系式y=x2﹣2x﹣3;
(2)设圆的半径为r,则直径MN=2r,
①当直线MN在x轴上方时,点N的坐标为(r+1,r),
代入抛物线解析式得,(r+1)2﹣2(r+1)﹣3=r,
整理得,r2﹣r﹣4=0,
解得r1=
 ,r2=
,r2=
 (舍去);
(舍去);
②当直线MN在x轴下方时,(r+1)2﹣2(r+1)﹣3=﹣r,
整理得,r2+r﹣4=0,
解得r3=
 ,r4=
,r4=
 (舍去),
(舍去),
所以该圆的半径为
 或
或
 ;
;
(3)①令y=0,则x2﹣2x﹣3=0,
解得x1=﹣1,x2=3,
∴点A(﹣1,0),B(3,0),
∴AB=3﹣(﹣1)=4,
∵MN=
 AB,
AB,
∴MN=
 ×4=3,
×4=3,
根据二次函数的对称性,点N的横坐标为1+
 =
=
 ,
,
代入二次函数解析式得,y=(
 )2﹣2×
)2﹣2×
 ﹣3=﹣
﹣3=﹣
 ,
,
∴点N的坐标为(
 ,﹣
,﹣
 ),
),
点F的纵坐标为﹣
 ,
,
∵点C关于点F的对称点为E,﹣
 ×2﹣(﹣3)=﹣
×2﹣(﹣3)=﹣
 ,
,
∴点E的坐标为(0,﹣
 ),
),
设直线BC的解析式为y=kx+b(k≠0,k、b为常数),
则
 ,
,
解得
 ,
,
∴直线BC的解析式为y=x﹣3,
x=1时,y=1﹣3=﹣2,
∴点D的坐标为(1,﹣2),
tan∠CED=
 =
=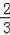
 ;
;
②∵直线BC的解析式为y=x﹣3,
∴∠BCO=45°,
若∠CDE=90°,则△CDE是等腰直角三角形,
∴点F与点D纵坐标相同,为﹣2,
∴点M的纵坐标为﹣2,
代入二次函数y=x2﹣2x﹣3得,x2﹣2x﹣3=﹣2,
整理得,x2﹣2x﹣1=0,
解得x1=1﹣
 ,x2=1+
,x2=1+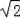
 ,
,
∵点M在第三象限,
∴点M的坐标为M(1﹣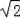
 ,﹣2);
,﹣2);
若∠CED=90°,则点E与点D的纵坐标相同,为﹣2,
∵点C关于点F的对称点为E,
∴点F的纵坐标为
 =﹣
=﹣
 ,
,
∴点M的纵坐标为﹣
 ,
,
代入二次函数y=x2﹣2x﹣3得,x2﹣2x﹣3=﹣
 ,
,
整理得,2x2﹣4x﹣1=0,
解得x1=1+
 ,x2=1﹣
,x2=1﹣
 ,
,
∵点M在第三象限,
∴点M的坐标为M(1﹣
 ,﹣
,﹣
 ),
),
综上所述,点M的坐标为(1﹣
 ,﹣2)或(1﹣
,﹣2)或(1﹣
 ,﹣
,﹣
 ).
).


【点评】本题是二次函数综合题型,主要考查了待定系数法求二次函数解析式,直线与圆的位置关系,锐角三角函数的定义,点的对称,综合性较强,但难度不大,难点在于要分情况讨论.


科目:初中数学 来源: 题型:
在△ABC中,其两个内角如下,则能判定△ABC为等腰三角形的是( )
A.∠A=40°,∠B=50° B.∠A=40°,∠B=60°
C.∠A=20°,∠B=80° D.∠A=40°,∠B=80°
查看答案和解析>>
科目:初中数学 来源: 题型:
初三年级教师对试卷讲评课中学生参与的深度与广度进行评价调查,其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项.评价组随机抽取了若干名初中学生的参与情况,绘制成如图所示的频数分布直方图和扇形统计图(均不完整),请根据图中所给信息解答下列问题:


(1)在这次评价中,一共抽查了 560 名学生;
(2)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为 54 度;
(3)请将频数分布直方图补充完整;
(4)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初三学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
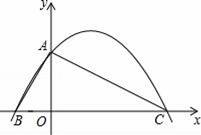
已知,如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点G是对称轴上一点,求当△GAB周长最小时,点G的坐标;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,并选择其中一个的加以说明;若不存在,说明理由;
(4)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A、B、M、N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com