
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°。

(1)求∠C的度数;
(2)求∠BED的度数.
(1)105°;(2)150°.
【解析】
试题分析:(1)∠C的度数=180°-∠A-∠ABC,因此应先求出∠ABC的度数;根据三角形的外角的性质可得,∠ABD=∠BDC-∠A=60°-45°=15°.再根据角平分线的定义可得,∠ABC=2∠ABD=2×15°=30°,从而可求∠C的度数
(2)求∠BED的度数,根据两直线平行,同旁内角互补得∠BED的度数.
试题解析:(1)∵∠BDC是△ABD的外角,
∴∠ABD=∠BDC-∠A=60°-45°=15°.
∵BD是△ABC的角平分线,
∴∠DBC=15°
∴∠ABC=2∠DBC=30°
∴∠C=180°-∠A-∠ABC=180°-45°-30°=105°;
(2)∵DE∥BC,
∴∠BDE=15°.
∴∠BED=180°-∠BDE-∠DBE=180°-15°-15°=150°.
考点: 1.三角形内角和;2.三角形的外角性质;3.角平分线的定义;4.平行线的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2016届江苏省兴化市七年级下学期期中考试数学试卷(解析版) 题型:解答题
如图①,△ABC的角平分线BD、CE相交于点P.
(1)如果∠A=70°,求∠BPC的度数;
(2)如图②,过P点作直线MN∥BC,分别交AB和AC于点M和N,试求∠MPB+∠NPC的度数(用含∠A的代数式表示);
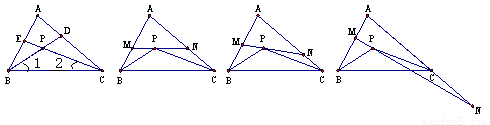
① ② ③ ④
在(2)的条件下,将直线MN绕点P旋转.
(ⅰ)当直线MN与AB、AC的交点仍分别在线段AB和AC上时,如图③,试探索∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由;
(ⅱ)当直线MN与AB的交点仍在线段AB上,而与AC的交点在AC的延长线上时,如图④,试问(ⅰ)中∠MPB、∠NPC、∠A三者之间的数量关系是否仍然成立?若成立,请说明你的理由;若不成立,请给出∠MPB、∠NPC、∠A三者之间的数量关系,并说明你的理由.
查看答案和解析>>
科目:初中数学 来源:2016届江苏省兴化市七年级下学期期中考试数学试卷(解析版) 题型:选择题
下列计算正确的是()
A.(a3)4=a7 B.a8÷a4=a2 C.(2a2)3·a3=8a9 D.4a5-2a5=2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com