
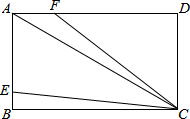
 如图,AC是矩形ABCD的对角线,AB=2,BC=2$\sqrt{3}$,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=$\frac{4\sqrt{3}}{3}$.
如图,AC是矩形ABCD的对角线,AB=2,BC=2$\sqrt{3}$,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=$\frac{4\sqrt{3}}{3}$. 分析 过点F作FG⊥AC于点G,证明△BCE≌△GCF,得到CG=CB=2$\sqrt{3}$,根据勾股定理得AC=4,所以AG=4-2$\sqrt{3}$,易证△AGF∽△CBA,求出AF、FG,再求出AE,得出AE+AF的值.
解答 解:过点F作FG⊥AC于点G,如图所示,
在△BCE和△GCF中,
$\left\{\begin{array}{l}{∠FGC=∠EBC=90°}\\{∠ACF=∠BCE}\\{CE=CF}\end{array}\right.$,
∴△BCE≌△GCF(AAS),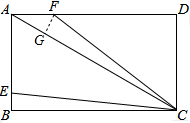 ∴CG=BC=2$\sqrt{3}$,
∴CG=BC=2$\sqrt{3}$,
∵AC=$\sqrt{A{B}^{2+}B{C}^{2}}$=4,
∴AG=4-2$\sqrt{3}$,
∵△AGF∽△CBA
∴$\frac{AG}{CB}=\frac{AF}{CA}=\frac{GF}{AB}$,
∴AF=$\frac{4(4-2\sqrt{3})}{2\sqrt{3}}$=$\frac{8\sqrt{3}-12}{3}$,
FG=$\frac{2(4-2\sqrt{3})}{2\sqrt{3}}$=$\frac{4\sqrt{3}-6}{3}$,
∴AE=2-$\frac{4\sqrt{3}-6}{3}$=$\frac{12-4\sqrt{3}}{3}$,
∴AE+AF=$\frac{12-4\sqrt{3}}{3}$+$\frac{8\sqrt{3}-12}{3}$=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题主要考查了三角形全等的判定和性质以及三角形相似的判定与性质,有一定的综合性,难易适中.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
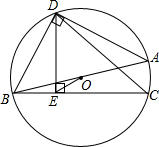 如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.
如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
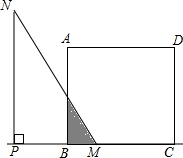 如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.
如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
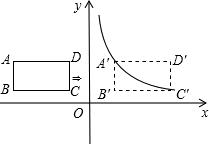 如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.
如图,在平面直角坐标系中,四边形ABCD是矩形,AD∥x轴,A(-3,$\frac{3}{2}$),AB=1,AD=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )
如图,在△ABC中,AB=AC,BC=24,tanC=2,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为( )| A. | 13 | B. | $\frac{15}{2}$ | C. | $\frac{27}{2}$ | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
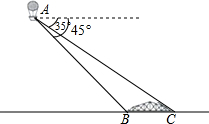 小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)
小明在热气球A上看到正前方横跨河流两岸的大桥BC,并测得B,C两点的俯角分别为45°,35°.已知大桥BC与地面在同一水平面上,其长度为100m,请求出热气球离地面的高度.(结果保留整数)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com