
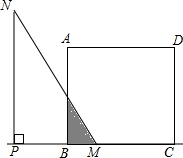
 如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.
如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.分析 ①当0≤x≤$\frac{2}{3}$$\sqrt{3}$时,根据正切的概念求出BE,得到y与x之间的函数关系式;
②当$\frac{2}{3}$$\sqrt{3}$≤x≤2时,根据正确的概念和梯形的面积公式求出y与x之间的函数关系式;
③当MN经过AB的中点时,根据BE=1,求出BM的长,求出y的值;
④假设存在x的值,根据题意进行解答,求出x,看是否符合条件.
解答 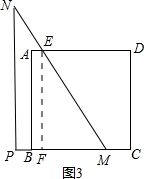
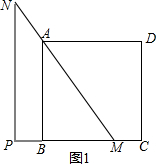 解:如图1,当MN经过点A时,
解:如图1,当MN经过点A时,
tan∠BAM=$\frac{BM}{AB}$,
∴BM=AB×tan30°=$\frac{2\sqrt{3}}{3}$,
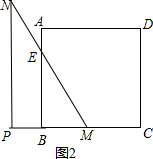
(1)如图2,当0≤x≤$\frac{2}{3}$$\sqrt{3}$时,
在Rt△EBM中,tan∠EMB=$\frac{BE}{BM}$,
∴BE=$\sqrt{3}$x,
y=$\frac{1}{2}$×x×$\sqrt{3}$x=$\frac{\sqrt{3}}{2}$x2,
故(1)不正确;
如图3,当$\frac{2}{3}$$\sqrt{3}$≤x≤2时,
作EF⊥BC于F,
则EF=AB=2,FM=$\frac{2\sqrt{3}}{3}$,
∴AE=BF=x-$\frac{2\sqrt{3}}{3}$,
y=$\frac{1}{2}$(x-$\frac{2\sqrt{3}}{3}$+x)×2=2x-$\frac{2\sqrt{3}}{3}$,
故(2)正确;
当MN经过AB的中点时,BE=1,
则BM=$\frac{\sqrt{3}}{3}$,
y=$\frac{1}{2}$×$\frac{\sqrt{3}}{3}$×1=$\frac{\sqrt{3}}{6}$,
故(3)不正确;
当y=$\frac{1}{2}$S正方形ABCD时,
2x-$\frac{2\sqrt{3}}{3}$=$\frac{1}{2}$×22,
解得,x=$\frac{3+\sqrt{3}}{3}$,符合题意,
故(4)正确,
故答案为:②④.
点评 本题考查的是几何变换,掌握正方形的性质和锐角三角函数的概念是解题的关键,在求函数解析式时,注意分情况讨论思想的正确运用.


科目:初中数学 来源: 题型:解答题
 用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).
用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
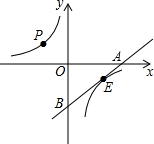 如图,点P(-2,3)在双曲线上,点E为该双曲线在第四象限图象上一动点,过E的直线与双曲线只有一个公共点,并与x轴和y轴分别交于A、B两点,则△AOB面积为( )
如图,点P(-2,3)在双曲线上,点E为该双曲线在第四象限图象上一动点,过E的直线与双曲线只有一个公共点,并与x轴和y轴分别交于A、B两点,则△AOB面积为( )| A. | 24 | B. | 12 | C. | 6 | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-3<b-3 | B. | a-b>0 | C. | $\frac{1}{3}a>\frac{1}{3}$b | D. | -2a<-2b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
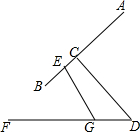 一台式电脑显示器的左视图如图所示,它由显示器侧边AB、支点四边形CEGD和底盘FD组成,若AB=28cm、EG=4$\sqrt{3}$cm,BE=3cm,∠EGF=60°,∠AEG=130°.若以FD所在直线为水平方向,求显示屏侧边AB相对于水平线FD的倾斜角度(用锐角表示).
一台式电脑显示器的左视图如图所示,它由显示器侧边AB、支点四边形CEGD和底盘FD组成,若AB=28cm、EG=4$\sqrt{3}$cm,BE=3cm,∠EGF=60°,∠AEG=130°.若以FD所在直线为水平方向,求显示屏侧边AB相对于水平线FD的倾斜角度(用锐角表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
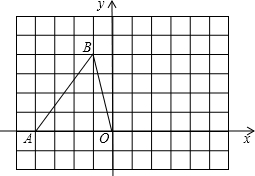 如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°
如图,在平面直角坐标系中,点A、B的坐标分别为A(-4,0),B(-1,4),将△AOB绕点O顺时针旋转90°查看答案和解析>>
科目:初中数学 来源: 题型:填空题
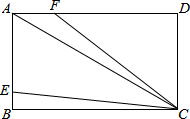 如图,AC是矩形ABCD的对角线,AB=2,BC=2$\sqrt{3}$,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=$\frac{4\sqrt{3}}{3}$.
如图,AC是矩形ABCD的对角线,AB=2,BC=2$\sqrt{3}$,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=$\frac{4\sqrt{3}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com