
【题目】(本题8分)某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
1 | 2 | 3 | 4 | 5 | 6 | |
李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
【答案】(1)2.51,2.51;(2)陈辉,理由参见解析;(3)选李超,理由参见解析.
【解析】
试题(1)此题是求算术平均数,分别将六个数据加在一起再除以6,就是李超和陈辉的平均成绩;(2)用方差公式求出每个人的方差,方差小的成绩稳定;(3)看训练数据,谁跳过2.55米可能性大,就选谁.
试题解析:(1)李超的平均成绩:(2.50+2.42+2.52+2.56+2.48+2.58)÷6=15.06÷6=2.51;陈辉的平均成绩:(2.54+2.48+2.50+2.48+2.54+2.52)÷6=15.06÷6=2.51;
(2)李超的方差:![]() =0.00277=2.77
=0.00277=2.77![]() ,
,
陈辉的方差:![]() =0.000633=6.33
=0.000633=6.33![]() ;
;
因为陈辉的方差小.所以陈辉的成绩稳定; (3)看训练数据,李超有两次次高过2.55,而陈辉一次也没有高过2.55的,所以选李超,因为他能跳过2.55米的可能性大.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=ax2+(![]() ﹣2a)x(a<0),下列说法正确的个数是( )
﹣2a)x(a<0),下列说法正确的个数是( )
①对于任何满足条件的a,该二次函数的图象都经过点(2,1)和(0,0)两点;
②若该函数图象的对称轴为直线x=x0,则必有1<x0<2;
③当x≥0时,y随x的增大而增大;
④若P(4,y1),Q(4+m,y2)(m>0)是函数图象上的两点,如果y1>y2总成立,则a≤﹣![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化。开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
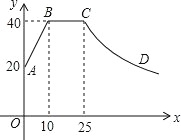
(1)分别求出线段AB和曲线CD的函数关系式;
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
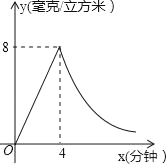
【题目】为了预防“流感”,某学校对教室采用药熏法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量y(毫克/立方米)与药物点燃后的时间x(分钟)成正比例,药物燃尽后,y与x成反比例(如图所示).已知药物点燃后4分钟燃尽,此时室内每立方米空气中含药量为8毫克.
(1)求药物燃烧时,y与x之间函数的表达式;
(2)求药物燃尽后,y与x之间函数的表达式;
(3)研究表明,当空气中每立方米的含药量不低于2毫克时,才能有效杀灭空气中的病菌,那么此次消毒有效时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的内心为I,外心为O
(1)试找出∠A与∠BOC,∠A与∠BIC的数量关系
(2)由(1)题的结论写出∠BOC与∠BIC的关系

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC于E点,连接DE交OC于F点,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.
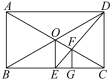
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com