
【题目】对于二次函数y=ax2+(![]() ﹣2a)x(a<0),下列说法正确的个数是( )
﹣2a)x(a<0),下列说法正确的个数是( )
①对于任何满足条件的a,该二次函数的图象都经过点(2,1)和(0,0)两点;
②若该函数图象的对称轴为直线x=x0,则必有1<x0<2;
③当x≥0时,y随x的增大而增大;
④若P(4,y1),Q(4+m,y2)(m>0)是函数图象上的两点,如果y1>y2总成立,则a≤﹣![]() .
.
A. 1个 B. 2个 C. 3个 D. 4个
【答案】B
【解析】
①把已知两点坐标代入二次函数,即可判断;
②根据题意,由①图像经过的两点可知, a<0,抛物线开口向下,得对称轴x0![]() ,即可作出判断;
,即可作出判断;
③根据二次函数的对称轴和增减性判断即可;
④根据二次函数的解析式求出抛物线对称轴x0=1-![]() ,由题意可得1-
,由题意可得1-![]() 4,解出即可判断.
4,解出即可判断.
①把(2,1)和(0,0)代入二次函数,等号成立,故对于任何满足条件的a,该二次函数的图象都经过点(2,1)和(0,0)两点符合题意,①正确;
②∵该二次函数的图象都经过点(2,1)和(0,0)两点,且a<0,抛物线开口向下,
∴对称轴x0![]() ,若该函数图象的对称轴为直线x=x0,则必有1<x0<2不符合题意,②错误;
,若该函数图象的对称轴为直线x=x0,则必有1<x0<2不符合题意,②错误;
③当x≥0时,根据二次函数的性质,y随x的增大而增大,到达顶点后,y随x的增大而减小,故当x≥0时,y随x的增大而增大不符合题意,③错误;
④若P(4,y1),Q(4+m,y2)(m>0)是函数图象上的两点,如果y1>y2总成立,说明抛物线对称轴x0=1-![]() 4,解得a
4,解得a![]() ﹣
﹣![]() ,④正确.
,④正确.
故选B.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】一个圆形喷水池的中心竖立一根高为![]() 顶端装有喷头的水管,喷头喷出的水柱呈抛物线形.当水柱与池中心的水平距离为
顶端装有喷头的水管,喷头喷出的水柱呈抛物线形.当水柱与池中心的水平距离为![]() 时,水柱达到最高处,高度为
时,水柱达到最高处,高度为![]() .
.
![]() 求水柱落地处与池中心的距离;
求水柱落地处与池中心的距离;
![]() 如果要将水柱的最大高度再增加
如果要将水柱的最大高度再增加![]() ,水柱的最高处与池中心的水平距离以及落地处与池中心的距离仍保持不变,那么水管的高度应是多少?
,水柱的最高处与池中心的水平距离以及落地处与池中心的距离仍保持不变,那么水管的高度应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C都在抛物线y=ax2﹣2amx+am2+2m﹣5(其中﹣![]() <a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
<a<0)上,AB∥x轴,∠ABC=135°,且AB=4.
(1)填空:抛物线的顶点坐标为 (用含m的代数式表示);
(2)求△ABC的面积(用含a的代数式表示);
(3)若△ABC的面积为2,当2m﹣5≤x≤2m﹣2时,y的最大值为2,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若a![]() +bx1=a
+bx1=a![]() +bx2且x1≠x2,则x1+x2=2,其中正确的有( )
+bx2且x1≠x2,则x1+x2=2,其中正确的有( )
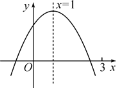
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣
x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣![]() x﹣
x﹣![]() 交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
(1)求抛物线的解析式;
(2)当点P在直线L下方时,过点P作PN∥y轴交L于点N,求PN的最大值.
(3)当点P在直线L下方时,过点P作PM∥x轴交L于点M,求PM的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=![]() (x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn.则S1+S2+S3+…+Sn=__.
(x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn.则S1+S2+S3+…+Sn=__.
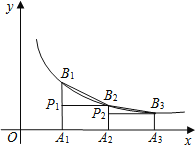
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
1 | 2 | 3 | 4 | 5 | 6 | |
李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD、CE分别是∠ABC、∠BCD的角平分线,则图中的等腰三角形有( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com