
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、
、![]() 在
在![]() 上,且
上,且![]() .
.

(1)求证:![]() ;
;
(2)求证![]() .
.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)设AB=a,则BD=DE=EC=a,DC=2a,在Rt△ABD中,AD=![]() a,由AD2=DE·DC,即
a,由AD2=DE·DC,即![]() =
=![]() ,又∠ADE=∠CDA,可证△ADE∽△CDA;
,又∠ADE=∠CDA,可证△ADE∽△CDA;
(2)由(1)知∠3=∠DAE,由三角形外角性质可得∠2+∠3=∠2+∠DAE=∠1,又AB=BD,∠B=90°,可得∠1=45°,所以∠1+∠2+∠3=90°.
证明:(1)∵AB=BD=DE=CE,设AB=a,则BD=DE=EC=a,DC=2a,
∵在Rt△ABD中,AD=![]() a,
a,
∴AD2=DE·DC,即![]() =
=![]() ,又∠ADE=∠CDA,
,又∠ADE=∠CDA,
∴△ADE∽△CDA;
(2)由(1)知∠3=∠DAE,
∴∠2+∠3=∠2+∠DAE=∠1,又AB=BD,∠B=90°,
∴∠1=45°,
∴∠1+∠2+∠3=90°


科目:初中数学 来源: 题型:
【题目】某校青年老师准备捐款3600元为敬老院的老年人购买一台电脑,这笔钱大家平均承担.实际捐款时又多了2名教师,因为购买电脑所需的总费用不变,于是每人少捐90元.问共有多少人参加捐款?原计划每人捐款多少元?.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学初三(1)班共有40名同学,在一次30秒跳绳测试中他们的成绩统计如下表:
跳绳数/个 | 81 | 85 | 90 | 93 | 95 | 98 | 100 |
人 数 | 1 | 2 | 8 | 11 | 5 |
将这些数据按组距5(个)分组,绘制成如图的频数分布直方图(不完整).
(1)将表中空缺的数据填写完整,并补全频数分布直方图;
(2)这个班同学这次跳绳成绩的众数是 个,中位数是 个;
(3)若跳满90个可得满分,学校初三年级共有720人,试估计该中学初三年级还有多少人跳绳不能得满分.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是正方形ABCD的对角线,BC=2,边BC在其所在的直线上平移,将通过平移得到的线段记为PQ,连接PA、QD,并过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)请直接写出线段BC在平移过程中,四边形APQD是什么四边形?
(2)请判断OA、OP之间的数量关系和位置关系,并加以证明;
(3)在平移变换过程中,设y=S△OPB,BP=x(0≤x≤2),求y与x之间的函数关系式,并求出y的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生综合素养的重要途径,某校为了解学生课外阅读情况,随机抽取若干名学生,调查他们平均每天课外阅读的时间(![]() 小时),并将收集的数据绘制成如图所示的两幅不完整的统计图表,请根据图表信息,解答下列问题:
小时),并将收集的数据绘制成如图所示的两幅不完整的统计图表,请根据图表信息,解答下列问题:
某校学生平均每天课外阅读时间频数表
类别 | 时间 | 频数(人) | 频率 |
A |
| 10 |
|
B |
| 20 | 0.4 |
C |
| 15 | 0.3 |
D |
|
|
|
某校学生平均每天课外阅读时间条形统计图

(1)填空:![]() ________,
________,![]()
![]() ________;并在图中补全条形统计图;
________;并在图中补全条形统计图;
(2)该校现有学生1200人,请你根据上述调查结果,估计该校学生平均每天课外阅读时间不少于1小时的共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
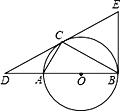
【题目】已知△ABC内接于以AB为直径的⊙O,过点C作⊙O的切线交BA的延长线于点D,且DA∶AB=1∶2.
(1)求∠CDB的度数;
(2)在切线DC上截取CE=CD,连接EB,判断直线EB与⊙O的位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,△ABC的三个顶点坐标分别为A(0,4),B(3,4),C(4,﹣1).
(1)试在平面直角坐标系中,画出△ABC;
(2)若△A1B1C1与△ABC关于x轴对称,写出A1、B1、C1的坐标;
(3)在x轴上找到一点P,使点P到点A、B两点的距离和最小;
(4)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“◇”和“☆”分别代表甲种植物和乙种植物,为了美化环境,采用如图所示的方案种植.
(1)观察图形,寻找规律,并填写下表:


(2)求出第![]() 个图形中甲种植物和乙种植物的株数;
个图形中甲种植物和乙种植物的株数;
(3)是否存在一种种植方案,使得乙种植物的株数是甲种植物的株数的2倍?若存在,请你写出是第几个方案,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com