
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化。开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
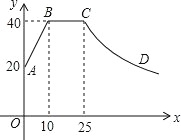
(1)分别求出线段AB和曲线CD的函数关系式;
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a-b+c>0;⑤若a![]() +bx1=a
+bx1=a![]() +bx2且x1≠x2,则x1+x2=2,其中正确的有( )
+bx2且x1≠x2,则x1+x2=2,其中正确的有( )
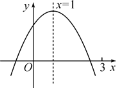
A. ①②③ B. ②④ C. ②⑤ D. ②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣
x2+bx+c经过点B(3,0)、C(0,﹣2),直线L:y=﹣![]() x﹣
x﹣![]() 交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
交y轴于点E,且与抛物线交于A、D两点,P为抛物线上一动点(不与A、D重合).
(1)求抛物线的解析式;
(2)当点P在直线L下方时,过点P作PN∥y轴交L于点N,求PN的最大值.
(3)当点P在直线L下方时,过点P作PM∥x轴交L于点M,求PM的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1,A2,A3,…An,…是x轴上的点,且OA1=A1A2=A2A3=…=An1An…=1,分别过点A1,A2,A3,…An,…作x轴的垂线交反比例函数y=![]() (x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn.则S1+S2+S3+…+Sn=__.
(x>0)的图象于点B1,B2,B3,…,Bn,…,过点B2作B2P1⊥A1B1于点P1,过点B3作B3P2⊥A2B2于点P2…,记△B1P1B2的面积为S1,△B2P2B3的面积为S2…,△BnPnBn+1的面积为Sn.则S1+S2+S3+…+Sn=__.
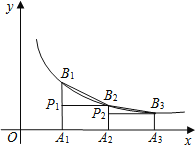
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数y1=x(x≥0),y2=![]() (x>0)的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3);②当x<3时,y2>y1;③当x=1时,BC=8;④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.其中正确结论的序号是( )
(x>0)的图象如图所示,则结论:①两函数图象的交点A的坐标为(3,3);②当x<3时,y2>y1;③当x=1时,BC=8;④当x逐渐增大时,y1随着x的增大而增大,y2随着x的增大而减小.其中正确结论的序号是( )
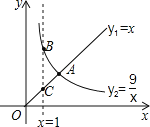
A. ①③④ B. ①②③④ C. ②③④ D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)某校初三(1)班进行立定跳远训练,以下是李超和陈辉同学六次的训练成绩(单位:m)
1 | 2 | 3 | 4 | 5 | 6 | |
李超 | 2.50 | 2.42 | 2.52 | 2.56 | 2.48 | 2.58 |
陈辉 | 2.54 | 2.48 | 2.50 | 2.48 | 2.54 | 2.52 |
(1)李超和陈辉的平均成绩分别是多少?
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?为什么?
(3)若预知参加级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数的图象经过(-2,-1),(1,1)两点,则下列关于此二次函数的说法正确的是【 】

A.y的最大值小于0 B.当x=0时,y的值大于1
C.当x=-1时,y的值大于1 D.当x=-3时,y的值小于0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com