
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.
【答案】(1)3;(2)![]() ;(3)n>0
;(3)n>0
【解析】
(1)观察已知表格中的对应值可知:该函数图象的开口向上,对称轴是直线x=1,由抛物线的对称性可知:x=3时的对应函数值与x= -1时的对应函数值相等,即可求得![]() 的值;
的值;
(2)把表中的三个点![]() 、(1,-1)、(2, 0)代入函数的解析式,得到关于a,b,c的方程组,即可求得解析式;
、(1,-1)、(2, 0)代入函数的解析式,得到关于a,b,c的方程组,即可求得解析式;
(3)根据函数的图象开口方向,增减性即可确定.
(1)观察已知表格中的对应值可知:该函数图象的开口向上,对称轴是直线x=1,
∴由抛物线的对称性可知:x=3时的对应函数值与x= -1时的对应函数值相等,即m的值为3;
(2)把![]() 、(1,-1)、(2, 0)代入二次函数
、(1,-1)、(2, 0)代入二次函数![]()
![]() ,得
,得
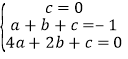 ,
,
解得: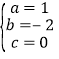
∴这个二次函数的解析式为![]() ;
;
(3)∵该函数图象的开口向上,对称轴是直线x=1,
∴若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,则
点A(n+2,y1),B(n,y2)在对称轴两侧时,n+2-1![]() 1-n且
1-n且![]() ,
,
解得:![]() ;
;
点A(n+2,y1),B(n,y2)在对称轴同侧(含顶点)时,![]() ,
,
综上可知:n的取值范围是n![]() .
.


科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,一节课40分钟中,学生的注意力随教师讲课的变化而变化。开始上课时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如图所示(其中AB,BC分别为线段,CD为双曲线的一部分):
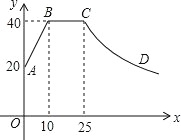
(1)分别求出线段AB和曲线CD的函数关系式;
(2)一道数学竞赛题,需要讲19分钟,为了效果较好,要求学生的注意力指标数最低达到36,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
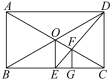
【题目】如图,在矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BC于E点,连接DE交OC于F点,作FG⊥BC于G点,则△ABC与△FGC是位似图形吗?若是,请说出位似中心,并求出相似比;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 C 为 Rt△ACB 与 Rt△DCE 的公共点,∠ACB=∠DCE=90°,连 接 AD、BE,过点 C 作 CF⊥AD 于点 F,延长 FC 交 BE 于点 G.若 AC=BC=25,CE=15, DC=20,则![]() 的值为___________.
的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据海峡导报报道,为推进漳州绿色农业发展, 2018-2020年,漳州市将完成农业绿色发展项目总投资414亿元。已知漳州2018年已完成项目投资100亿元,假设后两年该项目投资的平均增长率为x,依题意可列方程为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
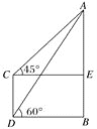
【题目】如图,某电视塔AB和楼CD的水平距离为100 m,从楼顶C处及楼底D处测得塔顶A的仰角分别为45°和60°,试求塔高为__________,楼高为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
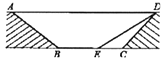
【题目】为缓解交通拥堵,某区拟计划修建一地下通道,该通道一部分的截面如图所示(图中地面![]() 与通道
与通道![]() 平行),通道水平宽度
平行),通道水平宽度![]() 为8米,
为8米, ![]() ,通道斜面
,通道斜面![]() 的长为6米,通道斜面
的长为6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的长为 米;
的长为 米;
(2)为增加市民行走的舒适度,拟将设计图中的通道斜面![]() 的坡度变缓,修改后的通道斜面
的坡度变缓,修改后的通道斜面![]() 的坡角为30°,求此时
的坡角为30°,求此时![]() 的长.(结果保留根号)
的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温州某企业安排65名工人生产甲、乙两种产品,每人每天生产2件甲或1件乙,甲产品每件可获利15元.根据市场需求和生产经验,乙产品每天产量不少于5件,当每天生产5件时,每件可获利120元,每增加1件,当天平均每件获利减少2元.设每天安排x人生产乙产品.
(1)根据信息填表
产品种类 | 每天工人数(人) | 每天产量(件) | 每件产品可获利润(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生产甲产品可获得的利润比生产乙产品可获得的利润多550元,求每件乙产品可获得的利润.
(3)该企业在不增加工人的情况下,增加生产丙产品,要求每天甲、丙两种产品的产量相等.已知每人每天可生产1件丙(每人每天只能生产一件产品),丙产品每件可获利30元,求每天生产三种产品可获得的总利润W(元)的最大值及相应的x值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com